P3260 [JLOI2014] 镜面通道
题目描述
在一个二维平面上,有一个镜面通道,由镜面 $AC, BD$ 组成,$AC, BD$ 长度相等,且都平行于 $x$ 轴,$B$ 位于 $(0,0)$。
通道中有 $n$ 个外表面为镜面的光学元件,光学元件 $\alpha$ 为圆形,光学元件 $\beta$ 为矩形(这些元件可以与其他元件和通道有交集,具体看下图)。光线可以在 $AB$ 上任一点以任意角度射入通道,光线不会发生削弱。当出现元件与元件,元件和通道刚好接触的情况视为光线无法透过(比如两圆相切)。
现在给出通道中所有元件的信息($\alpha$ 元件包括圆心坐标和半径 $x_i, y_i, r_i$,$\beta$ 元件包括左下角和右上角坐标 $x_1, y_1, x_2, y_2$)
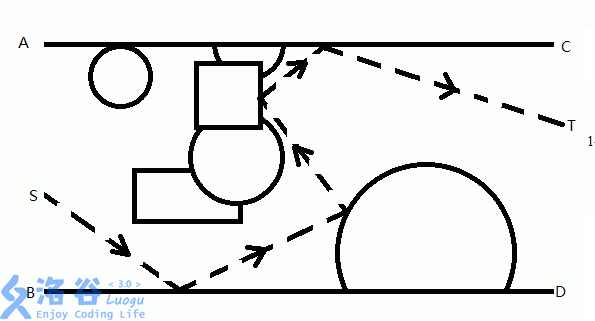
如上图,$S$ 到 $T$ 便是一条合法线路。

当然,显然存在光线无法透过的情况,现在交给你一个艰巨的任务,请求出至少拿走多少个光学元件后,存在一条光线线路可以从 $CD$ 射出。
下面举例说明:
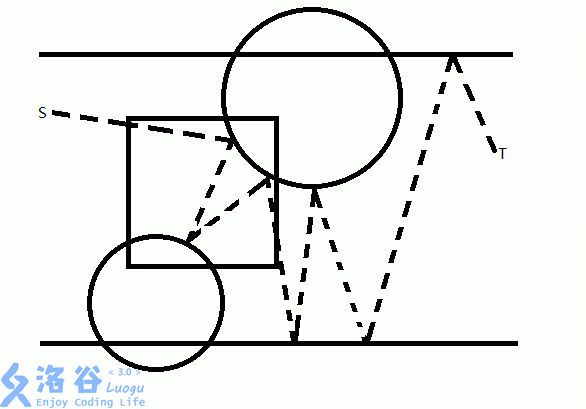
现在假设,取走中间那个矩形,那么就可以构造出一条穿过通道的光路,如图中的 $S$ 到 $T$。
输入格式
第一行包含两个整数,$x, y$,表示 $C$ 点坐标。
第二行包含一个数字 $n$,表示有 $n$ 个光学元件。
接下来 $n$ 行第一个数字如果是 $1$,表示元件 $\alpha$,后面会有三个整数 $x_i, y_i, r_i$ 分别表示圆心坐标和半径。第一个数字如果是 $2$,表示元件 $\beta$,后面会有四个整数 $x_1, y_1, x_2, y_2$ 分别表示左下角和右上角坐标。(矩形都平行,垂直于坐标轴)
输出格式
输出包含一行,至少需要拿走的光学元件个数 $m$。
说明/提示
$x\leq 10^5$,$y\leq 1000$,$n\leq 300$。