P3290 [SCOI2016] Go

Recently, Google’s Go AI—AlphaGo—defeated the former world champion Lee Sedol by a score of $4:1$, which is another milestone in the field of artificial intelligence. Unlike traditional search-based AI, AlphaGo uses the now very popular convolutional neural network model. In a convolutional neural network, every region of a specific size on the board is treated as a window. For example, if the board size is $5\times 6$ and the window size is $2\times 4$, then there are $12$ windows on the board. In addition, the model has some predefined templates whose size is the same as the window size. 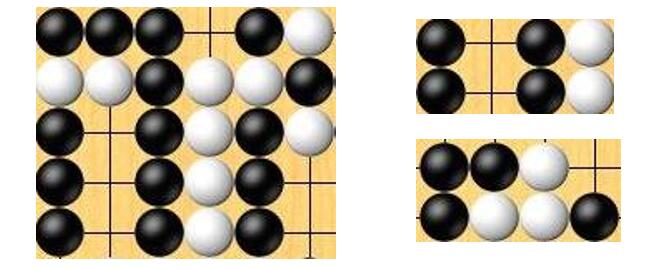The following figure shows a $5\times 6$ board and two $2\times 4$ templates:  For a template, as long as there exists a window on the board that matches it exactly, we say the template is activated; otherwise, the template is not activated. For example, in the figure the first template is activated, while the second one is not. The question we study is: for a given template, how many boards can activate it. To simplify the problem, we disregard all basic rules of Go and consider only an $n\times m$ board, where each position can only be one of three states: black stone, white stone, or empty. In other words, there are $3^{n\times m}$ such boards in total. In addition, we will give $q$ templates of size $2\times c$. We want to know, for each template, how many boards can activate it. Emphasis: templates always have exactly two rows.

The first line of input contains four positive integers $n, m, c$ and $q$, representing the number of rows of the board, the number of columns of the board, the number of columns of the template, and the number of templates, respectively. Then $2\times q$ lines follow; every consecutive two lines describe one template. Each line contains $c$ characters, and each character is one of ```W```, ```B``` or ```X```, representing white stone, black stone, or empty, respectively.

Output should contain $q$ lines, each with one integer, representing the number of boards that meet the requirement. Since the answer can be large, you only need to output the result modulo $10^9+7$.

For all test points: $1\leq n\leq 100$, $1\leq m\leq 12$, $1\leq c\leq 6$, $1\leq q\leq 5$. | Test point ID | Settings | | :----------: | :----------: | | $1$ | $n=3$, $m=4$, $c=2$ | | $2$ | $n=4$, $m=4$, $c=3$ | | $3$ | $n=2$, $m=9$, $c=6$ | | $4$ | $n=2$, $m=12$, $c=3$ | | $5$ | $n=2$, $m=12$, $c=5$ | | $6$ | $n=10$, $m=8$, $c=3$ | | $7$ | $n=10$, $m=10$, $c=5$ | | $8$ | $n=100$, $m=10$, $c=5$ | | $9$ | $n=100$, $m=12$, $c=5$ | | $10$ | $n=100$, $m=12$, $c=6$ | Translated by ChatGPT 5