P3301 [SDOI2013] Equation

Given the equation $x_1+x_2+\dots +x_{n}=m$. We impose restrictions on variables $1$ through $n_1$: $x_{1} \le a_{1},x_{2} \le a_{2},\dots, x_{n_1} \le a_{n_1}$. We impose restrictions on variables $n_1+1$ through $n_1+n_2$: $x_{n_1+1} \ge a_{n_1+1},x_{n_1+2} \ge a_{n_1+2},\dots,x_{n_1+n_2} \ge a_{n_1+n_2}$. Find the number of positive integer solutions of the equation under these restrictions. The answer can be large; please output it modulo $p$.

Multiple test cases. The first line contains two positive integers $T,p$. $T$ denotes the number of test cases in this file, and the meaning of $p$ is as described above. For each test case, the first line contains four non-negative integers $n,n_1,n_2,m$. The second line contains $n_1+n_2$ positive integers, denoting $a_{1},a_2,\dots, a_{n_1+n_2}$. Note that if $n_1+n_2$ equals $0$, this line will be empty.

Output $T$ lines, each containing a single integer representing the answer modulo $p$.

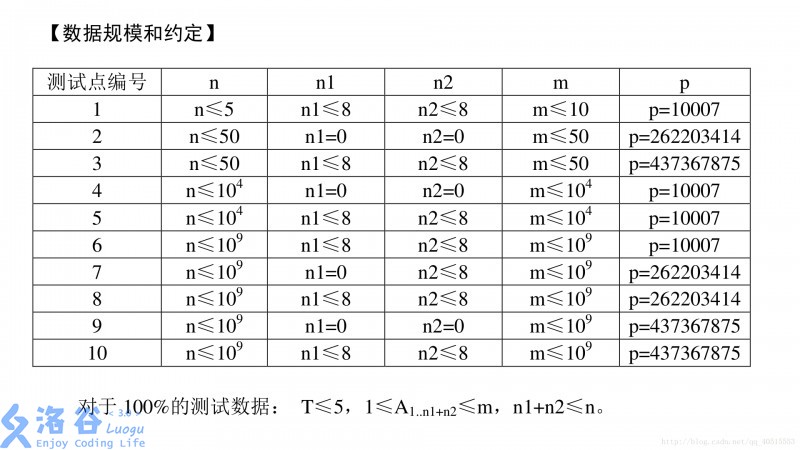
【Sample explanation】 For the first test case, the three solutions are $(1,3,2)$, $(1,4,1)$, $(2,3,1)$. For the second test case, the six solutions are $(1,1,3)$, $(1,2,2)$, $(1,3,1)$, $(2,1,2)$, $(2,2,1)$, $(3,1,1)$.  Constraints: For $100\%$ of the testdata, $1\le T \le 5$, $1\le m, n \le 10^9$, $1 \le a_i \le m$, $0 \le n_1,n_2 \le \min(8, m)$ and $n_1 + n_2 \le n$, $1\le p \le 437367875$. Translated by ChatGPT 5