P3351 [ZJOI2016] Resistor Network

Xiao Y is a very smart girl, but she can only compute the resistance between two nodes using series and parallel reductions. Now, given a resistor network, she wants to know how many pairs of vertices $u, v$ ($u \ne v$) have their resistance computable by series-parallel methods. We formalize when the resistance between a pair $u, v$ ($u \ne v$) can be computed using series-parallel methods. First, regard the resistor network as a graph with $n$ vertices and $m$ edges (each resistor corresponds to an edge). Let $S$ be the union of the vertices on all simple paths (paths that do not visit a vertex more than once) from $u$ to $v$. In other words, for a vertex $x$, if there exists a simple path from $u$ to $v$ that passes through $x$, then $x \in S$. If $S$ is nonempty and the induced subgraph of $S$ is a two-terminal series-parallel graph with terminals $u$ and $v$, then the resistance between $u$ and $v$ can be computed using series-parallel methods. 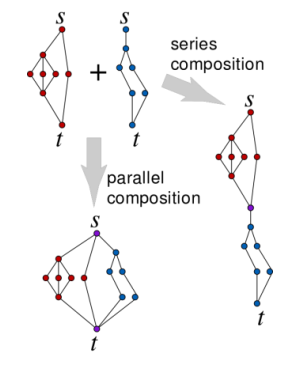A graph with two distinct terminals $s, t$ is called a two-terminal graph, where one is the source and the other is the sink. The parallel composition of two two-terminal graphs $X, Y$ builds a new graph by identifying their sources and their sinks, respectively. The series composition of two two-terminal graphs $X, Y$ builds a new graph by identifying the sink of $X$ with the source of $Y$. A graph formed from several two-terminal graphs consisting of two vertices and one edge, by a sequence of series and parallel compositions, is called a two-terminal series-parallel graph.  The induced subgraph of the set $S$ has vertex set $S$, and its edge set consists of edges in the original graph whose both endpoints lie in $S$.

The first line contains two positive integers $n, m$, the number of nodes and the number of resistors in the network. Each of the next $m$ lines contains two positive integers $u, v$ ($1 \le u, v \le n$, $u \ne v$), indicating there is a resistor between nodes $u$ and $v$.

Output a single line containing the answer: the number of vertex pairs whose resistance can be computed using series-parallel methods.

【Sample Explanation #1】 The feasible pairs are $(1, 2)$, $(1, 3)$, $(1, 4)$, $(2, 3)$, $(2, 4)$, $(5, 6)$. 【Constraints】 For 10% of the testdata, $n, m \le 10$, the original graph is connected and has no articulation point. For another 10% of the testdata, $n, m \le 100$, the original graph is connected and has no articulation point. For 30% of the testdata, $n, m \le 100$. For 40% of the testdata, $n, m \le 1000$. For another 30% of the testdata, the original graph is connected and has no articulation point. For 100% of the testdata, $1 \le n, m \le {10}^5$. Translated by ChatGPT 5