P3366 [Template] Minimum Spanning Tree

As stated, given an undirected graph, compute a minimum spanning tree. If the graph is disconnected, output `orz`.

The first line contains two integers $N,M$, representing that the graph has $N$ nodes and $M$ undirected edges. Then each of the next $M$ lines contains three integers $X_i,Y_i,Z_i$, indicating there is an undirected edge of length $Z_i$ connecting nodes $X_i$ and $Y_i$.

If the graph is connected, output a single integer equal to the sum of the edge lengths in the minimum spanning tree. If the graph is disconnected, output `orz`.

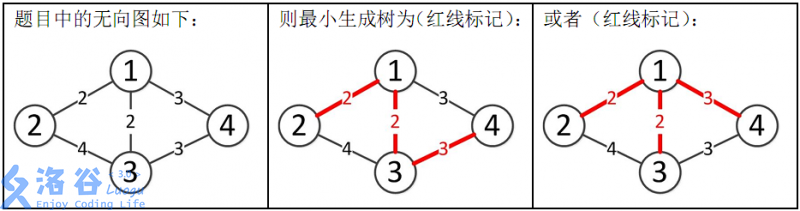
Constraints: - For 20% of the testdata, $N\le 5$, $M\le 20$. - For 40% of the testdata, $N\le 50$, $M\le 2500$. - For 70% of the testdata, $N\le 500$, $M\le 10^4$. - For 100% of the testdata, $1\le N\le 5000$, $1\le M\le 2\times 10^5$, $1\le Z_i \le 10^4$, $1\le X_i,Y_i\le N$. Sample explanation:  Therefore, the total edge weight of the minimum spanning tree is $2+2+3=7$. Translated by ChatGPT 5