P3376 [Template] Network Maximum Flow

As stated, given a network graph and its source and sink, compute the maximum flow of this network.

The first line contains four positive integers $n, m, s, t$, denoting the number of vertices, the number of directed edges, the index of the source, and the index of the sink, respectively. Each of the next $m$ lines contains three positive integers $u_i, v_i, w_i$, meaning that the $i$-th directed edge goes from $u_i$ to $v_i$ with capacity $w_i$ (i.e., the maximum flow on this edge is $w_i$).

One line containing a single positive integer, which is the maximum flow of the network.

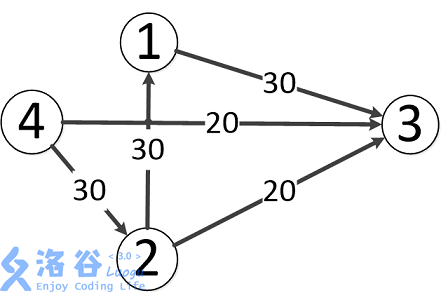
#### Explanation for Sample Input/Output 1  There are $3$ paths in the figure: - $4 \to 2 \to 3$, which can carry a flow of $20$. - $4 \to 3$, which can carry a flow of $20$. - $4 \to 2 \to 1 \to 3$, which can carry a flow of $10$ (edge $4 \to 2$ has already used $20$ units of flow beforehand). Therefore, the total flow is $20 + 20 + 10 = 50$. Output $50$. --- #### Constraints - For $30\%$ of the testdata, it is guaranteed that $n \le 10$, $m \le 25$. - For $100\%$ of the testdata, it is guaranteed that $1 \le n \le 200$, $1 \le m \le 5000$, $0 \le w < 2^{31}$. Translated by ChatGPT 5