P3382 Ternary Search

This problem may have severe precision issues and can be hard to pass on some testdata. The testdata is relatively weak and is for reference only.

As stated, you are given an $N$-th degree polynomial. It is guaranteed that within the interval $[l, r]$ there exists a point $x$ such that the function is monotonically increasing on $[l, x]$ and monotonically decreasing on $[x, r]$. Find the value of $x$.

The first line contains a positive integer $N$ and two real numbers $l, r$, as described above. The second line contains $N + 1$ real numbers, representing the coefficients of the $N$-th degree polynomial from highest degree to lowest.

Output one line containing a real number, which is the value of $x$. Your answer is considered correct if it satisfies either of the following: - Your answer $x'$ has a relative or absolute error not exceeding $10^{-5}$ compared to the standard answer $x$. - The function values corresponding to your answer and the standard answer, that is, $f(x')$ and $f(x)$, have a relative or absolute error not exceeding $10^{-5}$.

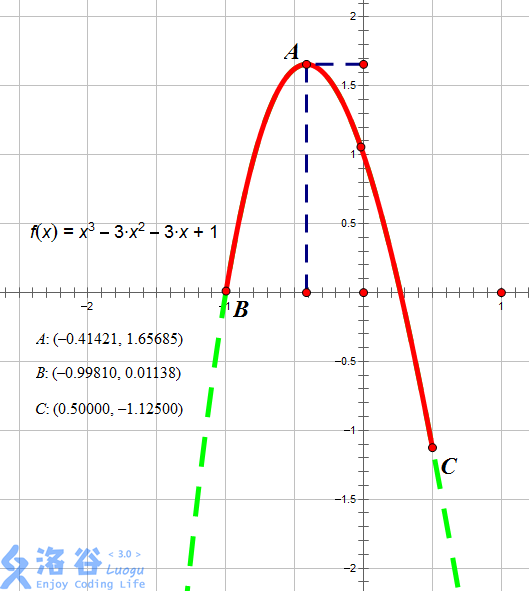
For $100\%$ of the testdata, $6 \le N \le 13$, the coefficients of the polynomial are in $[-100, 100]$ with up to $15$ decimal places, $|l|, |r| \le 10$ with up to $15$ decimal places, and $l \le r$. Sample Explanation:  As shown in the figure, the red segment is the graph of the function $f(x) = x^3 - 3 x^2 - 3x + 1$ on the interval $[-0.9981, 0.5]$. When $x = -0.41421$, the graph reaches its highest point, so the function is monotonically increasing on $[l, x]$ and monotonically decreasing on $[x, r]$. Therefore $x = -0.41421$, and the output is $-0.41421$. Translated by ChatGPT 5