P3509 [POI 2010] ZAB-Frog

On the bed of one particularly long and straight Byteotian brook there lie $n$ rocks jutting above the water level. Their distances from the brook's spring are $p_1 < p_2 < \cdots < p_n$ respectively. A small frog sitting on one of these is about to begin its leaping training. Each time the frog leaps to the rock that is the -th closest to the one it is sitting on. Specifically, if the frog is sitting on the rock at position $p_i$, then it will leap onto such $p_j$ that: $$ |\{ p_a : |p _ a - p _ i| < |p_j - p_i| \}| \le k \text{ and } |\{ p_a : |p _ a - p _ i| \le |p_j - p_i| \}| > k $$ If $p_j$ is not unique, then the frog chooses among them the rock that is closest to the spring. On which rock the frog will be sitting after $m$ leaps depending on the rock is started from?

The first line of the standard input holds three integers, $n$, $k$ and $m$ ($1 \le k < n \le 1 \, 000 \, 000, 1 \le m \le 10^{18}$), separated by single spaces, that denote respectively: the number of rocks, the parameter $k$, and the number of intended leaps. The second line holds $n$ integers $p_j$ ($1 \le p_1 < p_2 < \cdots < p_n \le 10^{18}$), separated by single spaces, that denote the positions of successive rocks on the bed of the brook.

Your program should print a single line on the standard output, with $n$ integers $r_1, r_2, \cdots, r_n$ from the interval $[1, n]$ in it, separated by single spaces. The number $r_i$ denotes the number of the rock that the frog ends on after making $m$ leaps starting from the rock no. $i$ (in the input order).

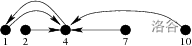
### 样例 #1 解释：  The figure presents where the frog leaps to (in a single leap) from each and every rock.