P3521 [POI 2011] ROT-Tree Rotations

You are given a binary tree with $n$ leaves. Each leaf has a weight $p_i$ (note: the root is not a leaf), and the weights of all leaves form a permutation of $1 \sim n$. For any node in this binary tree, it is guaranteed that it is either a leaf, or it has both left and right children. You may choose any set of nodes and swap their left and right subtrees. On the final tree, perform a preorder traversal of the whole tree and record the weights of the encountered leaves to form a permutation of length $n$. You need to minimize the number of inversions of this permutation.

The first line contains an integer $n$, the number of leaves. In the following lines, the tree is read recursively. When reading any subtree, start with its root. For a node $u$, first read an integer $x$ on a separate line. - If $x \neq 0$, then $u$ is a leaf and its weight is $x$. - If $x = 0$, then $u$ is an internal node; next read the information of its left subtree, and then the information of its right subtree.

Output a single integer, the minimal number of inversions.

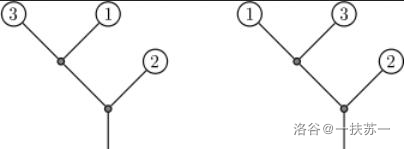
Explanation for Sample 1: In the figure below, the left is the initial tree, and the right is the tree after the operations.  Constraints: - For $30\%$ of the testdata, $n \leq 5 \times 10^3$. - For $100\%$ of the testdata, $2 \leq n \leq 2 \times 10^5$, $0 \leq x \leq n$, and the weights of all leaves form a permutation of $1 \sim n$. Note: Please note that $n$ is not the number of nodes in the tree. Translated by ChatGPT 5