P3535 [POI 2012] TOU-Tour de Byteotia
题目描述
**译自 POI 2012 Stage 2. Day 0「[Tour de Byteotia](https://szkopul.edu.pl/problemset/problem/mormqC6WwjeIiBpSNMhVbHni/site/?key=statement)」**
给定一个 $n$ 个点、$m$ 条边的**无向图**,问最少删掉多少条边能使得编号小于等于 $k$ 的点都不在任何一条简单环上。
输入格式
第一行包含三个整数 $n$、$m$、$k$,分别表示 $n$ 个节点, $m$ 条边,$k$ 意义见题面。
接下来 $m$ 行,每行两个整数 $u$、$v$,表示一条由 $u$ 到 $v$ 的**双向边**。数据保证**没有重边**。
输出格式
第一行一个整数 $cnt$,表示最少的删边数量;
接下来 $cnt$ 行,每行输出两个正整数 $a,b$,表示删除 $a,b$ 之间的一条边。先输出编号小的点,再输出编号大的点。
说明/提示
样例配图如下:
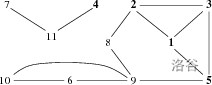
对于 $40\%$ 的数据,$n \le 1000$,$m \le 5000$。
对于 $100\%$ 的数据,$1 \le n \le 10^6$,$0 \le m \le 2\times10^6$,$1 \le k \le n$,$1 \le u \lt v \le n$。
翻译来自于 [LibreOJ](https://loj.ac/p/2693)。