P3535 [POI 2012] TOU-Tour de Byteotia

**Translated from POI 2012 Stage 2. Day 0 「[Tour de Byteotia](https://szkopul.edu.pl/problemset/problem/mormqC6WwjeIiBpSNMhVbHni/site/?key=statement)」.** Given an undirected graph with $n$ vertices and $m$ edges, find the minimum number of edges to delete so that all vertices with indices less than or equal to $k$ are not on any simple cycle.

The first line contains three integers $n$, $m$, and $k$, denoting $n$ vertices, $m$ edges, and $k$ as defined above. Then follow $m$ lines, each containing two integers $u$ and $v$, representing an undirected edge between $u$ and $v$. It is guaranteed that there are no multiple edges.

The first line contains an integer $cnt$, the minimum number of edges to delete. Then output $cnt$ lines, each containing two positive integers $a$ and $b$, indicating that the edge between $a$ and $b$ is deleted. Output the smaller vertex first, then the larger one.

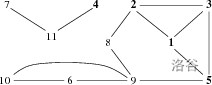
The sample illustration is as follows.  For $40\%$ of the testdata, $n \le 1000$, $m \le 5000$. For $100\%$ of the testdata, $1 \le n \le 10^6$, $0 \le m \le 2\times10^6$, $1 \le k \le n$, $1 \le u \lt v \le n$. Translated from [LibreOJ](https://loj.ac/p/2693). Translated by ChatGPT 5