P3576 [POI 2014] MRO-Ant colony

[English Edition](/paste/44plylwf)

Ants searching for food have come to a mountain. This mountain has $n$ caves and $n-1$ roads connecting these caves. In other words, all caves and roads form a tree. For each cave that is connected by exactly one road, there is an entrance that connects that cave to the outside. At each entrance, there are $g$ swarms of ants. The size of the $i$-th swarm is $m_i$. The swarms enter the mountain one after another; the next swarm enters if and only if there are no ants in the mountain. Once inside, the ants move as follows: - If a swarm enters a cave that is connected to $d$ roads (excluding the road they used to enter this cave), then the swarm splits into $d$ swarms of equal size, and each swarm chooses one road so that each road is taken by exactly one swarm. In particular, if $d=0$ (i.e., the swarm reaches an exit), the ants leave the mountain through that exit. - According to the above, if this swarm has $x$ ants, then each of the $d$ swarms has $\left\lfloor \dfrac{x}{d} \right\rfloor$ ants, and the remaining ants disappear (how they disappear is not important :)). 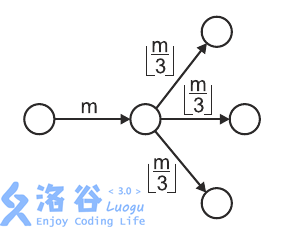The figure below shows an example: a swarm of size $m$ arrives at a cave that has $3$ roads (other than the one they came from), and the swarm splits into three swarms of size $\left\lfloor \dfrac{m}{3} \right\rfloor$ each.  On one of the roads, there is an anteater. Whenever a swarm passing along that road has size exactly $k$, it eats that entire swarm. Now, please compute how many ants the anteater eats in total.

The first line contains three integers $n, g, k$. The next line contains $g$ integers $m_1, m_2, \dots, m_g$. Then follow $n-1$ lines, each containing two integers $a, b$, indicating that there is an edge between $a$ and $b$. The first edge in the input is the edge where the anteater is located.

Output a single integer, the sum of the sizes of all eaten swarms.

For $100\%$ of the testdata, $2 \le n, g \le 10^6$, $1 \le k, m_i \le 10^9$, $1 \le a_i, b_i \le n$. Translated by ChatGPT 5