P3620 [APIO/CTSC2007] Data Backup

You work at an IT company backing up computer data for large office buildings. However, data backup is boring, so you want to design a system that lets different office buildings back up each other’s data while you sit at home enjoying computer games. All the office buildings are located on the same street. You decide to pair the buildings (two per group). Each pair can back up each other by laying a network cable between the two buildings. However, network cables are expensive. The local telecom company can provide only $K$ cables, which means you can arrange backups for only $K$ pairs of buildings (or a total of $2K$ buildings). Each building belongs to exactly one pair (in other words, those $2K$ buildings are all distinct). Additionally, the telecom company charges by the length of the cable in kilometers. Hence, you need to choose the $K$ pairs of buildings so that the total cable length is as short as possible. In other words, you need to choose the $K$ pairs so that the sum of the distances between each pair (the total distance) is minimized. Here is an example. Suppose you have $5$ clients whose buildings lie on a single street, as shown below. The $5$ buildings are located at distances $1\rm km$, $3\rm km$, $4\rm km$, $6\rm km$, and $12\rm km$ from the start of the street. The telecom company provides only $K=2$ cables.  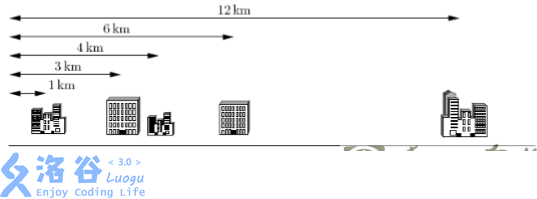In this example, the best pairing is to connect the $1$st and $2$nd buildings, and the $3$rd and $4$th buildings. This uses exactly $K=2$ cables as required. The length of the first cable is $\rm 3km-1km = 2km$, and the length of the second cable is $\rm 6km―4km = 2 km$. This pairing requires a total of $4\rm km$ of cable, achieving the minimum possible sum of distances.

The first line of input contains integers $N$ and $K$, where $N$ ($1 \leq N \leq 10^5$) is the number of office buildings, and $K$ ($\displaystyle 1\leq K \leq \frac{N}{2}$) is the number of cables available. Each of the next $N$ lines contains a single integer $s$ ($0 \leq s \leq 10^9$), the distance of each building from the start of the street. These integers are given in increasing order.

Output a single positive integer: the minimum total cable length required to connect $2K$ distinct buildings into $K$ pairs.

$30\%$ of the testdata satisfy $N \leq 20$. $60\%$ of the testdata satisfy $N \leq 10^4$. Translated by ChatGPT 5