P3621 [APIO2007] Wind Chime

You want to buy a gift for your younger brother Ike, but Ike has a special way of choosing gifts: he only likes things that he can arrange into an ordered shape. You plan to buy Ike a wind chime. A wind chime is a multi-layered ornament that is usually hung from the ceiling. Each wind chime consists of several horizontal bars connected by vertical strings. Each end of a bar has a string attached; below it hangs either another horizontal bar or a toy. 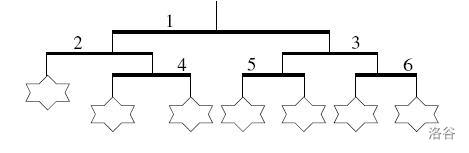Here is an example of a wind chime:  To satisfy Ike, you need to choose a wind chime that meets the following two conditions: 1. All toys are on the same level (that is, the number of bars between each toy and the ceiling is the same), or they differ by at most one level. 2. For any two toys that differ by one level, the left toy must hang lower than the right toy. A wind chime can be rearranged using the following rule: choose any bar and “swap” the strings at its two ends. That is, detach the strings from the left and right ends of the bar and reattach them to the opposite ends. This operation does not change the relative order of the strings on any bars below. As a trainee in informatics, you decide to design an algorithm to determine whether a given wind chime can be rearranged to satisfy Ike’s preferences. Consider the example above. The wind chime in the figure satisfies condition 1 but not condition 2 — the leftmost toy is higher than the one to its right. However, we can transform this wind chime into one that Ike likes through the following steps: 1. First, swap the left and right ends of bar $1$, which swaps the positions of bars $2$ and $3$. 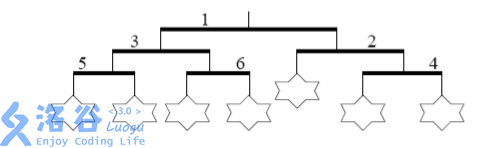The result is shown below:  2. Second, and final, swap the left and right ends of bar $2$, which moves bar $4$ to the left and moves the toy that was on the left to the right. The result is shown below:  Now this wind chime satisfies Ike’s conditions. Your task is: given a description of a wind chime, compute the minimum number of swaps needed to make it satisfy Ike’s conditions (if possible).

The first line contains an integer $n$, the number of bars in the wind chime. The next $n$ lines describe the connections of the bars. The $i$-th of these lines contains two integers $l_i$ and $r_i$, separated by a space, describing what is attached to the left and right ends of bar $i$. If a toy is attached, the value is ``-1``; otherwise, it is the index of the bar hanging below.

Output a single integer: the minimum number of swaps needed to make the wind chime satisfy Ike’s conditions. If it is impossible, output ``-1``.

Constraints - For $100\%$ of the testdata, $1 \le n \le 10^5$, $-1 \le l_i, r_i \le n$, and $l_i, r_i \ne 0$. Translated by ChatGPT 5