P3622 [APIO2007] Zoo

The newly built circular zoo is the pride of the Asia-Pacific region. The zoo stands on a small island in the Pacific Ocean and consists of a large ring of enclosures, each containing one species of animal. As shown below:  You are the zoo’s public manager. Your job is to make every visitor as happy as possible. Today a group of children is visiting the zoo, and you hope they will have a wonderful time there. But this is not easy — some animals are liked by some children, while others are feared by some children. For example, Alex likes the cute monkeys and koalas but is afraid of sharp-toothed lions. Polly, however, likes lions because of their beautiful manes but is afraid of smelly koalas. You may choose to remove some animals from their enclosures so that the children are not scared. However, you cannot remove too many animals, or the children will have nothing to see. Each child stands outside the circular ring of enclosures and can see $5$ consecutive enclosures. You are given, for each child, which animals they like and which they fear. A child is happy if at least one of the following holds: - At least one animal they fear is removed. - At least one animal they like is not removed. 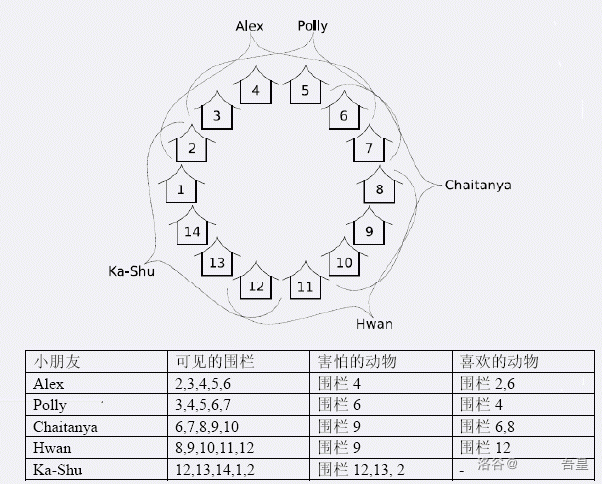For example, consider the children and animals shown below:  - Suppose you remove the animals in enclosures 4 and 12. Alex and Ka-Shu will be happy because at least one animal they fear has been removed. This also makes Chaitanya happy because the animals he likes in enclosures 6 and 8 both remain. However, Polly and Hwan will not be happy because they cannot see any animals they like, and the animals they fear are still there. This arrangement makes three children happy. - Now try another plan: if you remove the animals in enclosures 4 and 6, Alex and Polly will be happy because the animals they fear have been removed. Chaitanya will also be happy: although the animal he likes in enclosure 6 is removed, he can still see the animal he likes in enclosure 8. Similarly, Hwan is happy because he can see the animal he likes in enclosure 12. The only unhappy child is Ka-Shu. - If you remove only the animal in enclosure 13, Ka-Shu will be happy because one animal he fears has been removed, and Alex, Polly, Chaitanya, and Hwan will also be happy because each of them can see at least one animal they like. Thus $5$ children are happy. This plan makes the maximum number of children happy.

The first line contains two integers $N$, $C$, separated by a space. $N$ is the number of enclosures ($10 \le N \le 10^4$), and $C$ is the number of children ($1 \le C \le 5 \times 10^4$). The enclosures are numbered clockwise as $1, 2, 3, \cdots, N$. Each of the next $C$ lines describes one child in the following format: $E, F, L, X_1, X_2, \cdots, X_F, Y_1, Y_2, \cdots, Y_L$. Here, $E$ is the index of the first enclosure this child can see ($1 \le E \le N$). In other words, the child can see enclosures $E$, $E+1$, $E+2$, $E+3$, and $E+4$. Note that if the numbering exceeds $N$, it wraps around starting from $1$ again. For example, when $N=14$ and $E=13$, the enclosures the child can see are $13, 14, 1, 2$, and $3$. $F$ is the number of animals this child fears. $L$ is the number of animals this child likes. Enclosures $X_1, X_2, \cdots, X_F$ contain animals the child fears. Enclosures $Y_1, Y_2, \cdots, Y_L$ contain animals the child likes. $X_1, X_2, \cdots, X_F, Y_1, Y_2, \cdots, Y_L$ are pairwise distinct integers, and all referenced enclosures are among the five enclosures the child can see. The children are listed in nondecreasing order of their $E$ values (that is, the child with the smallest $E$ appears first, and the one with the largest $E$ appears last). Note that there may be multiple children with the same $E$.

Output a single integer: the maximum number of children that can be made happy.

Constraints For $100\%$ of the testdata, $10 \le N \le 10^4$, $1 \le C \le 5 \times 10^4$, $1 \le E \le N$. Sample Explanation - In the first sample (the example from the statement), all $C=5$ children can be made happy. - In the second sample, it is impossible to make all $C=7$ children happy. Translated by ChatGPT 5