P3623 [APIO2008] Free Roads

The kingdom of New Asia has $N$ villages connected by $M$ roads. Some roads are cobblestone, while others are cement. Keeping roads toll-free requires a large expense, and it seems impossible for the kingdom to keep all roads free. Therefore, a new road maintenance plan is urgently needed. The king has decided to keep as few roads free as possible, but there must be exactly one path consisting of free roads between any two distinct villages. At the same time, although cement roads are better suited to modern traffic, the king also thinks that walking along cobblestone roads is interesting. So the king decides to keep exactly $K$ cobblestone roads free. For example, suppose the villages and roads in New Asia are as shown in Figure 3(a). If the king wants to keep two cobblestone roads free, one possible plan is to keep roads $(1, 2)$, $(2, 3)$, $(3, 4)$, and $(3, 5)$ free, as shown in Figure 3(b). This plan satisfies the king’s requirements because: 1. There is a path consisting of free roads between any two villages. 2. The number of free roads is as small as possible. 3. There are exactly two cobblestone roads, $(2, 3)$ and $(3, 4)$, in the plan.  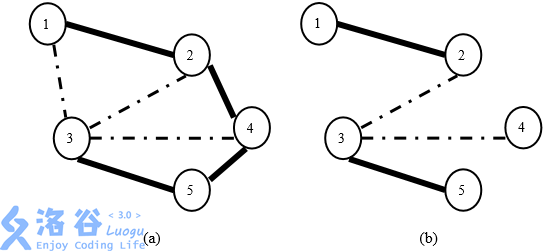Figure 3: (a) An example of villages and roads in New Asia. Solid lines denote cement roads, and dashed lines denote cobblestone roads. (b) A maintenance plan that keeps two cobblestone roads free. Only the free roads are shown. Given a description of the villages and roads in New Asia and the number of cobblestone roads the king wants to keep free, write a program to determine whether there exists a road maintenance plan that satisfies the king’s requirements. If it exists, output any one such plan.

The first line of input contains three integers separated by spaces: $N$, the number of villages $(1 \le N \le 2 \times 10^4)$; $M$, the number of roads $(1 \le M \le 10^5)$; $K$, the number of cobblestone roads the king wants to keep free $(0 \le K \le N - 1)$. The following $M$ lines describe the roads in New Asia, numbered from $1$ to $M$. The $(i+1)$-th line describes the $i$-th road with 3 space-separated integers: $u_i$ and $v_i$, the indices of the two villages connected by the $i$-th road, where villages are numbered from $1$ to $N$; $c_i$, indicating the type of the $i$-th road. $c_i = 0$ means the $i$-th road is a cobblestone road, and $c_i = 1$ means the $i$-th road is a cement road. It is guaranteed that between any pair of villages there is at most one connecting road.

If no road maintenance plan satisfies the king’s requirements, your program should print `no solution` on the first line. Otherwise, your program should output a valid road maintenance plan, i.e., the list of roads to remain free. Output the free roads in the same way as they are given in the input. If there are multiple valid plans, you may output any one of them.

Constraints For $100\%$ of the testdata, it is guaranteed that $1 \le N \le 2 \times 10^4$, $1 \le M \le 10^5$, $0 \le K \le N - 1$. Translated by ChatGPT 5