P3629 [APIO2010] Patrol

In a region, there are $n$ villages, numbered $1, 2, \dots, n$. There are $n-1$ roads connecting these villages. Each road connects exactly two villages, and from any village you can reach any other village via these roads. Each road has length $1$ unit. To ensure safety, a patrol car must patrol all roads every day. The police station is located in village $1$. Every day the patrol car always starts from the police station and finally returns to the police station. The figure below shows a region with $8$ villages, where villages are represented by circles (village $1$ is the black circle) and roads are the line segments connecting the circles. To traverse all the roads, the patrol car needs to travel a distance of $14$ units, and each road must be traversed twice.  To reduce the total patrol distance, the region plans to build $K$ new roads between the villages, and each new road can connect any two villages. Two new roads may meet at or end at the same village, as in figure (c) below. A new road can even be a loop, i.e., both ends connect to the same village. Due to limited budget, $K$ can only be $1$ or $2$. Meanwhile, to avoid wasting funds, every day the patrol car must traverse each newly built road exactly once. 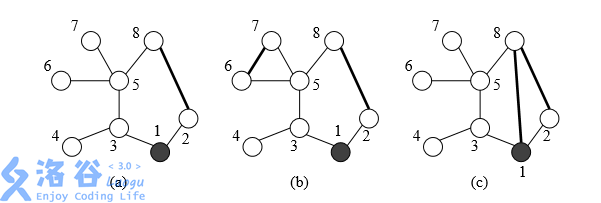The following are some examples:  In (a), one new road is built, and the total distance is $11$. In (b), two new roads are built, and the total patrol distance is $10$. In (c), two new roads are built, but since the patrol car must traverse each new road exactly once, the total distance becomes $15$. Write a program that reads the information about the roads between villages and the number of roads to be built, computes the best plan for adding new roads to minimize the total patrol distance, and outputs this minimum patrol distance.

The first line contains two integers $n, K(1 ≤ K ≤ 2)$. Then follow $n-1$ lines, each with two integers $a,b$, indicating that there is a road between villages $a$ and $b$ $(1 ≤ a, b ≤ n)$.

Output a single integer, the minimum total patrol distance after adding $K$ new roads.

- In $10\%$ of the testdata, $1≤n≤1000,K=1$. - In $30\%$ of the testdata, $K=1$. - In $80\%$ of the testdata, the number of adjacent villages for each village does not exceed $25$. - In $90\%$ of the testdata, the number of adjacent villages for each village does not exceed $150$. - In $100\%$ of the testdata, $3≤n≤10^5,1≤K≤2$. Translated by ChatGPT 5