P3635 [APIO2012] 苦无

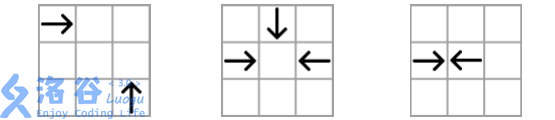
苦无 (Kunai) 是一种忍者使用的形状像刀的武器，忍者通过投掷苦无攻击对手。现在有 $N$ 名忍者聚集在一块 $H$ 行 $W$ 列的棋盘式的广场上。每个忍者都站在其所在方块的中心处，任何两个忍者都不在同一个方块上。每个忍者都拿着一个苦无，面朝上、下、左、右四个方向中的一个方向站着。在时刻 $0$，所有忍者同时向其所朝向的方向投掷苦无。 每个苦无将会一直保持其初始的方向，并以单位速度飞行。如果某个时刻一个位置上多于一个的苦无，它们将会相撞并且消失。苦无特别小，可以看成质点。同时，由于忍者的移动速度特别快，他们不会被苦无击中。 在下面的例子中，我们用箭头来表示苦无，而箭头的方向即为苦无的方向。在这些图中，所有的苦无都会相撞后消失。  在下面的图中，两个粗线箭头表示的苦无不会相撞。其中在第二个和第三个图中，其中一个粗线表示的苦无会与细线表示的苦无相撞后消失，因此不会撞上另一个粗线表示的苦无。  你的任务是计算经过足够长的时间之后，在这个 $W × H$ 的广场中有多少格子被苦无经过。

第一行包含两个被空格隔开的整数 $W$, $H$，表示广场的尺寸为 $W$ 列 $H$ 行。第二行包含一个整数 $N$，表示忍者的数量。 接下来 $N$ 行中，第 $i$ 行有三个以空格分隔的整数 $X_i, Y_i, D_i$, 表示第 $i$ 个忍者处在从左往右的 $X_i$ 列、从上往下的第 $Y_i$ 行，任何两个忍者不在同一个位置。第 $i$ 个忍者面向的方向由 $D_i$ 表示，分别为： - $D_i = 0$，表示忍者向右； - $D_i = 1$，表示忍者向上； - $D_i = 2$，表示忍者向左； - $D_i = 3$，表示忍者向下。

输出一个整数，表示经过足够长的时间之后，在这个 $W × H$ 的广场中被苦无经过的格子数量。

对于全部数据，忍者数 $1 \le N \le 10^5$，列数 $1 \le W \le 10^9$，行数 $1 \le H \le 10^9$； 坐标范围 $1 \le X_i \le W$，$1 \le Y_i \le H$。 - 在 $10\%$ 的数据中，$N \le 1000$, $W \le 1000$, $H \le 1000$。 - 在 $40\%$ 的数据中，$N \le 1000$。