P3635 [APIO2012] Kunai

Kunai is a knife-shaped weapon used by ninjas, who attack by throwing it. There are $N$ ninjas gathered on a chessboard-like plaza with $H$ rows and $W$ columns. Each ninja stands at the center of a cell, and no two ninjas share the same cell. Each ninja holds one kunai and faces one of the four directions: up, down, left, or right. At time $0$, all ninjas simultaneously throw their kunai in the direction they are facing. Each kunai keeps its initial direction and flies at unit speed. If, at some moment, more than one kunai is at the same position, they collide and disappear. Kunai are very small and can be treated as point masses. Also, because ninjas move extremely fast, they will not be hit by any kunai. 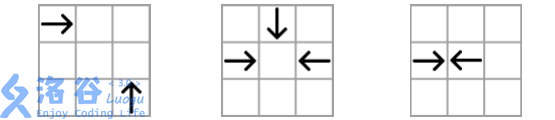In the following example, we use arrows to represent kunai, and the direction of an arrow is the direction of the corresponding kunai. In these figures, all kunai collide and disappear.  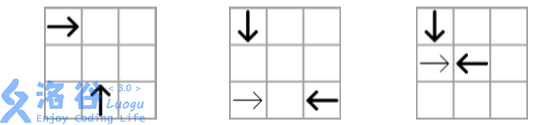In the figures below, the two bold arrows represent kunai that will not collide. In the second and third figures, one of the bold-arrow kunai collides with a thin-arrow kunai and disappears, so it will not collide with the other bold-arrow kunai.  Your task is to compute, after sufficient time has passed, how many cells in this $W \times H$ plaza are traversed by at least one kunai.

The first line contains two integers $W$, $H$ separated by a space, indicating the plaza has $W$ columns and $H$ rows. The second line contains an integer $N$, the number of ninjas. The next $N$ lines each contain three integers $X_i$, $Y_i$, $D_i$ separated by spaces. The $i$-th ninja is at column $X_i$ (counted from left to right) and row $Y_i$ (counted from top to bottom). No two ninjas share the same position. The facing direction of the $i$-th ninja is given by $D_i$: - $D_i = 0$: facing right; - $D_i = 1$: facing up; - $D_i = 2$: facing left; - $D_i = 3$: facing down.

Output one integer: after sufficient time has passed, the number of cells in the $W \times H$ plaza that are traversed by at least one kunai.

For all testdata, $1 \le N \le 10^5$, $1 \le W \le 10^9$, $1 \le H \le 10^9$; coordinate ranges are $1 \le X_i \le W$, $1 \le Y_i \le H$. - In $10\%$ of the testdata, $N \le 1000$, $W \le 1000$, $H \le 1000$. - In $40\%$ of the testdata, $N \le 1000$. Translated by ChatGPT 5