P3636 Surface

xht likes studying mathematical functions, and he especially likes the inverse proportional function.

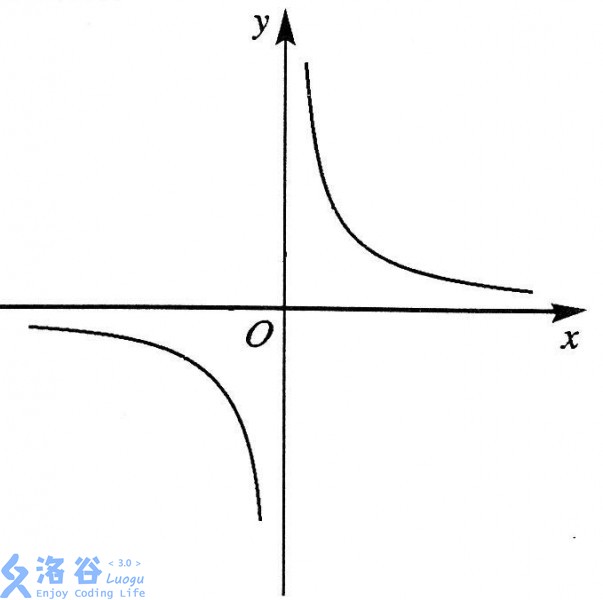
We know that the graph of the inverse proportional function $xy = a$ is a hyperbola.  xht then wondered: what would it look like if we extend it to three dimensions? Define the surface $C(k)$ as the surface determined by the equation $xyz = k$. Define the aesthetic value $P(k)$ of the surface as the sum of the squares of the Manhattan distances to the origin of all lattice points (points whose $x$, $y$, and $z$ coordinates are all integers) on $C(k)$. (The Manhattan distance from $(x, y, z)$ to the origin is $|x| + |y| + |z|$.) Now, xht arranges the surfaces $\{C(a), C(a+1), \dots, C(b)\}$ in a row. You are required to compute the sum of their aesthetic values, that is $P(a) + P(a+1) + \dots + P(b)$, modulo $10007$.

One line containing two positive integers $a$, $b$.

One line containing a single integer. 

Explanation of Sample 1: On the surface $xyz = 3$, there are $12$ lattice points: $(1, 1, 3)$, $(1, 3, 1)$, $(3, 1, 1)$, $(-1, -1, 3)$, $(-1, -3, 1)$, $(-3, -1, 1)$, $(1, -1, -3)$, $(1, -3, -1)$, $(3, -1, -1)$, $(-1, 1, -3)$, $(-1, 3, -1)$, $(-3, 1, -1)$. The sum of the squares of their Manhattan distances to the origin is $5^2 \times 12 = 300$. Constraints: - For $20\%$ of the testdata, $a = b \le 100$. - For another $40\%$ of the testdata, $a, b \le 3 \times 10^5$. - For $100\%$ of the testdata, $1 \le a, b \le 3 \times 10^8$. Translated by ChatGPT 5