P3640 [APIO2013] Problem Setter

All kinds of programming contests are flourishing nowadays. Designing a good contest is by no means easy; for example, creating testdata for problems is a challenge. A good set of testdata should differentiate between different programs: programs that meet all requirements should naturally get full score, while those that look correct may fail on some special data. In this problem, your role in the contest is reversed. As a seasoned programmer, you will help the Happy Programmer Contest problem-setting committee design the testdata for this contest. The committee chose two graph problems, split into $8$ subtasks. They wrote some code that seems to solve these subtasks. When designing testdata, the committee expects some of these source programs to receive full score, while others should get $0$ or only a small amount of partial score. You will be given these source programs (C, C++, Pascal versions). For each subtask, you need to produce a dataset $X$ that distinguishes the two given source programs $A$ and $B$ for that subtask. More specifically, the generated data must satisfy the following two conditions: - On input $X$, source program $A$ will definitely not exceed the time limit (TLE). - On input $X$, source program $B$ will definitely exceed the time limit (TLE). In addition, the committee prefers small-scale testdata and hopes the testdata contains at most $T$ integers. In this problem, we only care whether source programs $A$ and $B$ time out; we do not care whether their results are correct. The problem-setting committee chose two graph problems as the contest tasks: Single-Source Shortest Path (SSSP) and a problem called the “Mystery” problem. We list the pseudocode completed by the committee in the appendix, and the specific C, C++ and Pascal source programs are included in the provided files. Subtasks See the table below. Each row describes one subtask. The first six subtasks are related to SSSP, and subtasks 7 and 8 are related to the Mystery problem. The score of each subtask is shown in the table.  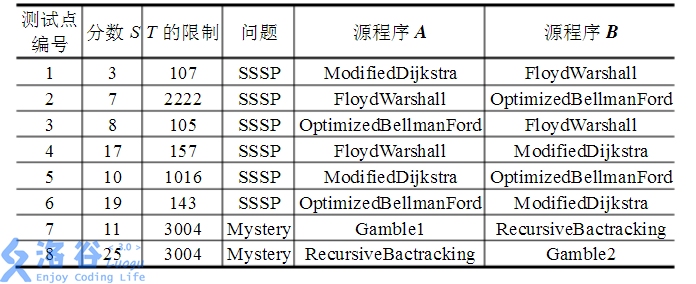For each subtask, the input $X$ produced by your program must be able to distinguish the source programs $A$ and $B$ for that task; only then can you get the corresponding score. Specifically, your score is determined by the number of integers in $X$. Suppose $X$ contains $F$ integers, the full score of the subtask is $S$, and $T$ is the target size for that task. Then the score for this test will be given by: $$S \times \min\{T / F, 1\}.$$ That is, if your testdata $X$ contains at most $T$ integers, you will receive the full score for that subtask. You need to name your $8$ test files as 1.txt ~ 8.txt. For each subtask data $X$, the judging system will determine your score according to the following steps: - If no data is submitted, you receive no score. - If the data does not meet the input format requirements, you receive no score. - Run source program $A$ on the input; if a timeout occurs, you receive no score. - Run source program $B$ on the input; if a timeout occurs, the score for this test is given by the formula above. All provided source programs maintain a counter to count the number of operations performed by the program. During execution, when this counter exceeds $10^6$, we consider the program to have timed out. Problem 1: Single-Source Shortest Path (SSSP) Given a weighted directed graph $G$ and two vertices $s$ and $t$ in $G$, let $p(s, t)$ be the length of the shortest path from $s$ to $t$ in $G$. If $s$ and $t$ are not connected, then $p(s, t) = 10^9$. In this problem, the input is the graph $G$ and $Q$ queries $(s_1, t_1), (s_2, t_2), \dots, (s_Q, t_Q)$. The output is the corresponding values $p(s_1, t_1), p(s_2, t_2), \cdots, p(s_Q, t_Q)$ for these $Q$ queries. Problem 2: Mystery Given an undirected graph $G$ with $V$ vertices and $E$ edges, you are required to assign labels to all vertices (labels range from $[0, X-1]$), such that any two adjacent vertices have different labels. Find the minimum feasible $X$. Appendix: Pseudocode Below is the pseudocode for all programs we provide; the variable counter roughly describes the running time of the programs. The C++ versions of these pseudocode programs will be used for judging. FloydWarshall ```cpp // pre-condition: the graph is stored in an adjacency matrix M counter = 0 for k = 0 to V-1 for i = 0 to V-1 for j = 0 to V-1 increase counter by 1; M[i][j] = min(M[i][j], M[i][k] + M[k][j]); for each query p(s,t) output M[s][t]; ``` OptimizedBellmanFord ```cpp // pre-condition: the graph is stored in an adjacency list L counter = 0 for each query p(s,t); dist[s] = 0; // s is the source vertex loop V-1 times change = false; for each edge (u,v) in L increase counter by 1; if dist[u] + weight(u,v) < dist[v] dist[v] = dist[u] + weight(u,v); change = true; if change is false // this is the ’optimized’ Bellman Ford break from the outermost loop; output dist[t]; ``` ModifiedDijkstra ```cpp // pre-condition: the graph is stored in an adjacency list L counter = 0; for each query p(s,t) dist[s] = 0; pq.push(pair(0, s)); // pq is a priority queue while pq is not empty increase counter by 1; (d, u) = the top element of pq; remove the top element from pq; if (d == dist[u]) for each edge (u,v) in L if (dist[u] + weight(u,v) ) < dist[v] dist[v] = dist[u] + weight(u,v); insert pair (dist[v], v) into the pq; output dist[t]; ``` Gamble1 ```cpp Sets X = V; labels vertex i in [0..V-1] with i; Sets counter = 0; // will never get TLE ``` Gamble2 ```cpp Sets X = V; labels vertex i in [0..V-1] with i; Sets counter = 1000001; // force this to get TLE ``` RecursiveBacktracking ```cpp This algorithm tries X from 2 to V one by one and stops at the first valid X. For each X, the backtracking routine label vertex 0 with 0, then for each vertex u that has been assigned a label, the backtracking routine tries to assign the smallest possible label up to label X-1 to its neighbor v, and backtracks if necessary. // Please check RecursiveBacktracking.cpp/pas to see // the exact lines where the iteration counter is increased by 1 ```

Problem 1 The input consists of two parts. The first part uses an adjacency list to describe the weighted directed graph $G$. The second part describes shortest path queries on $G$. - The first line of the first part contains an integer $V$, the number of vertices in $G$. All vertices are labeled $0, 1, \cdots, V - 1$. - The next $V$ lines each describe all outgoing edges of one vertex. In the $i$-th line, the first integer $n_i$ is the out-degree of vertex $i$. Then there are $n_i$ integer pairs $(j, w)$, each indicating a directed edge from $i$ to $j$ with weight $w$. The first line of the second part contains an integer $Q$, the number of queries. Then follow $Q$ lines. In the $k$-th line, there are two integers $s_k$ and $t_k$, the source and the target of that query. Any two adjacent integers on the same line must be separated by at least one space. In addition, the data must satisfy the following constraints: - $0 < V \leq 300$, $n_i$ is a non-negative integer, $0 \leq j < V$, $\lvert w \rvert < 10^6$, $0 \leq \sum\limits_{i = 0}^{V-1} n_i \leq 5000$, $0 < Q \leq 10$, $0 \leq s_k < V$, $0 \leq t_k < V$. - The graph contains no negative-weight cycles. Problem 2 - The first line contains two integers $V$ and $E$. - Then follow $E$ lines; each line contains two integers $a$ and $b$, indicating that $a$ and $b$ are adjacent in $G$. In addition, the input must satisfy the following constraints: - $70 < V < 1000$, $1500 < E < 10^6$. - For every edge $(a, b)$, we have $a \neq b$, $0 \leq a < V$, $0 \leq b < V$, and no edge is repeated.

Problem 1 The program will output $Q$ lines, one integer per line, representing the corresponding $p(s_k, t_k)$. At the very end, all provided programs will print the value of the counter for this input. Problem 2 The program will output $X$ in the first line, i.e., the minimum label range. In the second line, it will output $V$ integers, giving the labels of vertices $0$ to $V - 1$ in order. At the very end, all provided programs will print the value of the counter for this input.

Source code is in the attachment. Thanks to zhouyonglong for modifying the SPJ. Translated by ChatGPT 5