P3642 [APIO2016] Fireworks Show

A fireworks show is one of the most eye-catching festival activities. In the show, all fireworks must explode at the same time. For safety, the fireworks are placed away from the switch and connected to the switch by fuses. The fuses form a tree, and the fireworks are the leaves, as shown in the figure. A spark starts at the switch and travels along the fuses. Whenever the spark reaches a junction, it splits and continues burning along all incident fuses. The burning speed of every fuse is a fixed constant. The figure shows the layout connecting six fireworks $\{E_1, E_2, \dots, E_6\}$ and the length of each fuse. It also shows the explosion time of each firework when the spark is ignited at time $0$ at the switch.  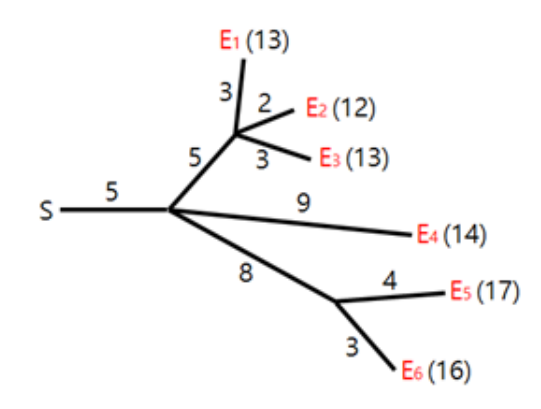Hyunmin designed the fuse layout for the fireworks show. Unfortunately, in his design, the fireworks do not necessarily explode simultaneously. We want to adjust some fuse lengths so that all fireworks explode at the same time. For example, to make all fireworks in the figure explode at time $13$, we can adjust the fuse lengths as shown on the left below. Similarly, to make all fireworks explode at time $14$, we can adjust the lengths as shown on the right.  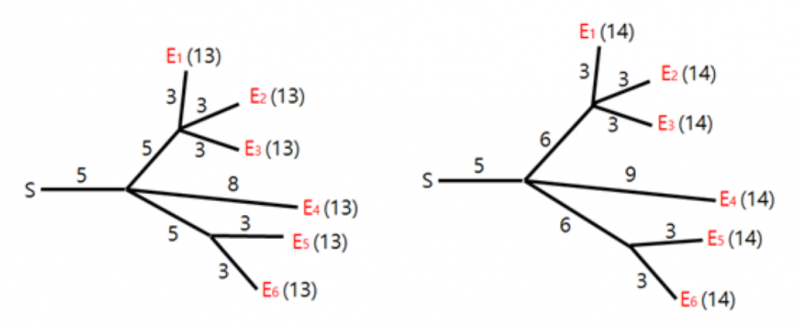The cost of modifying a fuse is the absolute difference between its new length and its original length. For example, changing the top layout to the layout on the left below has a total cost of $6$, while changing it to the layout on the right has a total cost of $5$. Fuse lengths may be reduced to $0$ without changing the connectivity. Given a fuse layout, write a program to adjust the fuse lengths so that all fireworks explode at the same time, while minimizing the total cost.

All input values are positive integers. Let $N$ be the number of junctions, and $M$ be the number of fireworks. Junctions are numbered from $1$ to $N$, where junction $1$ is the switch. Fireworks are numbered from $N + 1$ to $N + M$. The first line contains $N, M$. Each of the next $N + M - 1$ lines describes one edge. For every node $v$ with $2 \leq v \leq N + M$, the line for $v$ gives two integers $P_v, C_v$, where $1 \leq P_v < v$ specifies the junction to which node $v$ is connected, and $C_v$ is the length of the connecting fuse ($1 \leq C_v \leq 10^9$). Except for the switch, every junction is connected to more than $1$ fuse, and each firework is connected to exactly $1$ fuse.

Output the minimum total cost to adjust the fuse lengths so that all fireworks explode simultaneously.

Constraints - Subtask 1 (7 points): $N = 1$, $1 \leq M \leq 100$. - Subtask 2 (19 points): $1 \leq N + M \leq 300$, and the distance from the switch to any firework is at most $300$. - Subtask 3 (29 points): $1 \leq N + M \leq 5000$. - Subtask 4 (45 points): $1 \leq N + M \leq 300000$. Translated by ChatGPT 5