P3681 [CERC2016] Dancing Disks

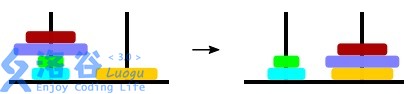
Luka is very good at solving the Tower of Hanoi problem, and he invented a similar game that uses disks and pegs. The game has $n$ disks of different sizes and $36$ pegs. The disks are numbered from $1$ to $n$ from smallest to largest. The pegs form a $6 \times 6$ grid: rows are numbered $1$ to $6$ from top to bottom, and columns are numbered $1$ to $6$ from left to right.  At the beginning, all $n$ disks are stacked on the peg at $(1,1)$. In each move, you may choose a peg, take the top several disks, then choose some peg to its right in the same row or some peg below it in the same column, and place all the taken disks on top of that peg (their order is preserved; they are not reversed). The goal is to move all disks to $(6,6)$, with strictly decreasing sizes from bottom to top. Given the initial configuration, find any sequence of moves that completes the game. It is guaranteed that a solution exists.

The first line contains a positive integer $n$ ($1 \le n \le 40000$), the number of disks. The second line contains $n$ positive integers $d_1, d_2, \cdots, d_n$ ($1 \le d_i \le n$), listing from bottom to top the labels of the disks on the peg at $(1,1)$. It is guaranteed that no two disks have the same label.

Output $m$ lines, where $m$ is the number of moves in your solution. In the $i$-th line, output $4$ items $r_i, c_i, p_i, n_i$, meaning that in the $i$-th move you choose the top $n_i$ ($n_i \ge 1$) disks from $(r_i, c_i)$ and move them in direction $p_i$. If you move to the right, then $p_i$ is `R`; if you move downward, then $p_i$ is `D`. If there are multiple valid solutions, output any one.

Translated by ChatGPT 5