P3689 [ZJOI2017] Polynomial

Kotori Itsuka recently studied the properties of polynomials with coefficients modulo 2. She found that one can obtain a very long string using multiplication of polynomials modulo 2: For an $n$-degree polynomial $f\left( x \right)$ with coefficients 0 or 1, we compute $g\left( x \right) = f\left( x \right)^{m}$ modulo 2. Then $g\left( x \right)$ is an $nm$-degree polynomial with $nm + 1$ coefficients. Writing these coefficients from the highest degree to the lowest degree gives a 01 string of length $nm + 1$. For example, for the polynomial $f\left( x \right) = x^{3} + x + 1$, we compute $g\left( x \right) = f\left( x \right)^{3} = x^{9} + x^{7} + x^{6} + x^{5} + x^{2} + x^{1} + 1$, thus we obtain a string of length 10: 1011100111. Now given a polynomial $f\left( x \right)$ of degree $n$, integers $m$, $L$, $R$, and a 01 string $t$ of length $K$. Let $s$ be the string obtained from $f\left( x \right)^{m}$, and let $s\left[ L, R \right]$ denote the substring from the $L$-th character to the $R$-th character of $s$. Kotori wants to know how many times $t$ appears in $s\left[ L, R \right]$.

The first line contains an integer $T$ denoting the number of test cases. For each test case, the first line contains five integers $n, m, K, L, R$. The second line contains a 01 string of length $n + 1$ representing the coefficients of the polynomial $f\left( x \right)$. The $i$-th character represents the coefficient of degree $n - i + 1$ of $f\left( x \right)$. The third line contains a string of length $K$ representing the string $t$.

For each test case, output a single integer denoting the answer.

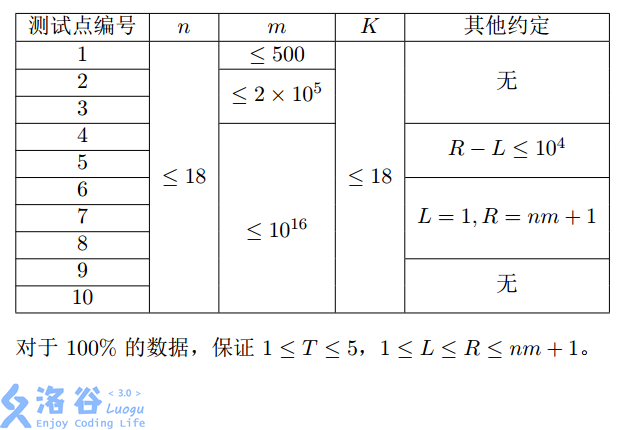
Time and Space Limit Time limit: 3 s, Memory limit: 512 MB. Constraints  Translated by ChatGPT 5