P3729 Manhattan Project EX

- Manhattan Project EX, The X Makes It Sound Cool. - After Aiden hacked into DedSec’s system, he discovered that the nuclear launch had entered its countdown. He must stop the launch process. 

- Aiden has a computer network. Each computer has an insane configuration of at least Intel Xeon E50 v40 + 40-way GTX10800Titan, and they are connected directly or indirectly by wireless links, which can be represented by an undirected connected graph. However, his network is not secure enough: DedSec may attack it and cut some wireless links, causing the network to become disconnected. To prevent this, Aiden decides to select some computers as computing nodes, and use the others as relay nodes, to carry out the task of stopping the nuclear launch. Although every machine is high-end, there are differences between knockoff parts and genuine parts—each computer has a different work capacity, denoted $ w_{i}$. Now Aiden wants to know: given a required work capacity, what is the maximum safety coefficient of the entire network? - Let the given graph be $G = (V , E)$, where $V$ = $V_{1}$ (computing nodes) + $V_{2}$ (relay nodes). - We define the safety coefficient $k$ as the largest $k$ such that for any two vertices $u, v \in V_{1}$, there are at least $k$ edge-disjoint paths from $u$ to $v$ (edge-disjoint means no repeated edges; repeated vertices are allowed). - We define the total work capacity of the selected nodes as $W = \sum_{v \in V_{1}}{w_{v}}$. - Constraints: - For 30% of the testdata, $qn^{4}$ is no greater than 1e8. - For 100% of the testdata, $n \le 550$, $m \le 3000$, $q \le 2017$, and each query and $w_{i}$ are no more than $10^{6}$. - All numbers are positive integers.

- The first line contains three integers $n, m, q$, the number of computers, wireless links, and queries. - The second line contains $n$ integers, the $w_{i}$ of the computers. - Lines 3 to $m+2$: each line contains two integers $u, v$, indicating a direct wireless link between $u$ and $v$; no other guarantees. - Lines $m+3$ to $m+q+2$: each line contains one integer $K$, representing the required total work capacity for that query.

- Output $q$ lines. For each query, output one integer: under the requirement that the total work capacity is at least $K$, the maximum safety coefficient of the network. If the requirement can be met using only one computer, output "nan". - If it is impossible to meet the requirement, output "Nuclear launch detected". - Outputting only "nan" will not score.

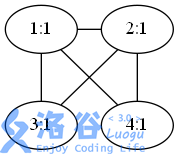
 - For query 1, choosing any single computer as a computing node is a valid solution. - For query 2, at least three computers must be selected; any three form a valid solution. The three selected vertices form a triangle; for any two vertices there are two ways to reach each other (clockwise and counterclockwise along the triangle), so the answer is 2. - For query 3, selecting all computers is still insufficient. Translated by ChatGPT 5