P3740 [HAOI2014] Posters

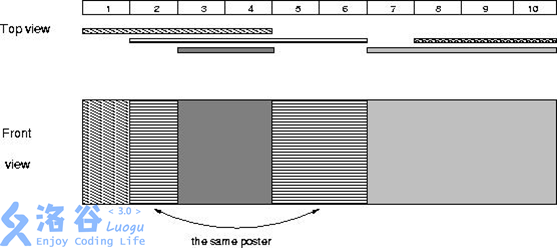
The city of Bytetown is holding a mayoral election, and all voters can freely express their opinions about the candidates. For unified management, the city committee has prepared an electoral wall for voters to post posters. The posting rules are as follows: 1. The electoral wall is a rectangle of length $N$ units, with each unit being a cell. 2. The height of every posted poster must be the same as the height of the electoral wall. 3. Each poster is denoted by `A B`, meaning it covers from cell $A$ to cell $B$. 4. A later poster may cover earlier posters or parts of them. Please determine how many posters are still visible on the electoral wall after all posters have been posted.

The first line contains two positive integers $N$ and $M$, the length of the electoral wall and the number of posters, respectively. Each of the next $M$ lines contains two positive integers $A_i$ and $B_i$, denoting the position covered by a poster. All numbers are positive integers, separated by a single space.

Output the number of posters that remain visible after all posters have been posted.

 **Constraints** $10 \le N \le 10000000$, $1 \le M \le 1000$, $1 \le A_i \le B_i \le 10000000$. Translated by ChatGPT 5