P3756 [CQOI2017] Old C's Blocks

Old C (Lao C) is a programmer. As a lazy programmer, Old C often plays a block game on his computer to kill time. The game is played on a grid with $R$ rows and $C$ columns of unit cells. Two cells are called adjacent if they share a side, and among adjacent pairs, some shared edges are marked as special. These special edges follow a very regular pattern. First, in row $1$, the edge between the first two cells is a special edge. Then, the special edges have period $4$ in the horizontal direction and period $2$ in the vertical direction. Between every odd-numbered column and the next column there are special edges, and the parity of the rows carrying these edges alternates from left to right. 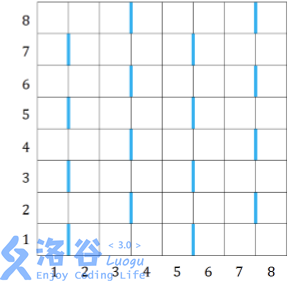The figure below shows a grid with $R = C = 8$, where the special edges are marked in blue. First, in row $1$, the edge between column $1$ and column $2$ is special. Because the vertical period is $2$, the edge between column $1$ and column $2$ is special in all odd-numbered rows. Because the horizontal period is $4$, the edge between column $5$ and column $6$ is also special in all odd-numbered rows; if the grid is large enough, so are the edges between columns $9$ and $10$, $13$ and $14$, etc. Because every odd-numbered column and the next column have special edges, the edges between columns $3$ and $4$, and between $7$ and $8$, are also special; since the row parity alternates from left to right, these special edges lie in even-numbered rows. If the grid is larger, we can find all special edges in the same way.  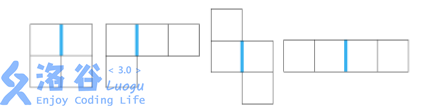Each cell can hold exactly one block. At the beginning of the game, some cells already contain blocks, while others are empty. Old C hates the pattern shown below. If he finds some blocks arranged in that hated shape (the positions of the special edges must also match those in the figure), he will immediately rage quit. Even if the hated shape appears after any number of rotations or reflections, he will still rage quit.  To avoid rage quitting, Old C decides to remove some blocks while he still can, so that the remaining blocks cannot form the hated shape. However, removing a block costs some coins, and the cost may differ from block to block. Of course, Old C wants to spend as few coins as possible. What is the minimum total number of coins needed? Old C is too lazy to think about it and leaves the problem to you.

The first line contains three positive integers $C, R, n$, meaning that in a grid with $C$ columns and $R$ rows, there are $n$ cells that contain blocks. Each of the next $n$ lines contains three positive integers $x, y, w$, meaning that the cell at column $x$, row $y$ contains a block, and removing it costs $w$ coins. All entries are distinct and within the grid.

Output one line containing a single integer, the minimum total number of coins required.

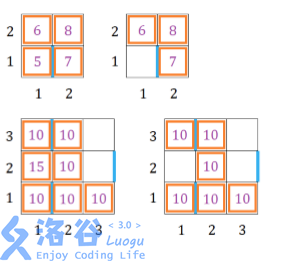
[Explanation for Sample 2] As shown in the figure. It is easy to see that if we do not remove the block at column 1, row 2, then we must remove at least two blocks to avoid containing the hated shape, costing at least 20 coins; whereas after deleting the block at column 1, row 2, all existing hated shapes disappear, and we only need to spend 15 coins.  Constraints For test points $1 \sim 2$, $1 \leq C, R \leq 100$, $1 \leq n \leq 20$. For test points $3 \sim 6$, $1 \leq C, R \leq 10^5$, $2000 \leq n \leq 5000$, with graded testdata. For test points $7 \sim 10$, $1 \leq C, R \leq 10^5$, $30000 \leq n \leq 10^5$, with graded testdata. For all test points, $1 \leq C, R, n \leq 10^5$, $1 \leq w \leq 10^4$. Translated by ChatGPT 5