P3772 [CTSC2017] Game

Xiao R and his roommate Xiao B are playing a game in their dorm. They play a total of $n$ games, and each game ends with either Xiao R winning or Xiao B winning. In game 1, the probability that Xiao R wins is $p_1$, and the probability that Xiao B wins is $1 - p_1$. Except for the first game, in each game the probability that Xiao R wins depends on whether Xiao R won the previous game. Specifically: 1. If in game $i − 1$ ($1 < i ≤ n$) Xiao R won, then in game $i$ the probability that Xiao R wins is $p_i$, and the probability that Xiao B wins is $1 − p_i$. 2. If in game $i − 1$ ($1 < i ≤ n$) Xiao B won, then in game $i$ the probability that Xiao R wins is $q_i$, and the probability that Xiao B wins is $1 − q_i$. Xiao D often comes to watch Xiao R and Xiao B play, so he knows the outcomes of some games. He wants to know, under the information he currently knows, what the expected total number of games won by Xiao R is among the $n$ games. Xiao D does not have a good memory: sometimes he recalls the outcome of some game and adds it to his known information; sometimes he forgets a previously remembered outcome and removes it from his known information. Your task is: whenever Xiao D adds or deletes one piece of information, compute, based on Xiao D’s current known information, the expected total number of games won by Xiao R among the $n$ games. Note: If Xiao D forgets the result of a game and later recalls it again, the two remembered outcomes are not necessarily the same. You do not need to care whether his memory matches the actual situation; you only need to compute the answers according to his memory.

The first line contains two positive integers $n, m$ and a string $\textrm{type}$. They indicate that Xiao R and Xiao B play $n$ games in total, Xiao D performs $m$ operations of modifying his known information, and the data is of type $\textrm{type}$. The string $\textrm{type}$ is provided to help obtain partial scores; you may not need this input. See [Constraints] for its meaning. The next $n$ lines: the 1st line contains a real number $p_1$, meaning that in the first game the probability that Xiao R wins is $p_1$. Line $i$ ($1 < i ≤ n$) contains two real numbers $p_i, q_i$. Here, $p_i$ means that if Xiao R won game $i − 1$, then in game $i$ the probability that Xiao R wins is $p_i$; $q_i$ means that if Xiao B won game $i − 1$, then in game $i$ the probability that Xiao R wins is $q_i$. The next $m$ lines each describe one change to Xiao D’s known information. There are two types of operations. 1. `add i c` means Xiao D recalls the outcome of game $i$ and adds it to his known information. If $c = 0$ it means Xiao B won game $i$; if $c = 1$ it means Xiao R won game $i$. It is guaranteed that $i, c$ are integers with $1 ≤ i ≤ n, 0 ≤ c ≤ 1$. If this is not the first operation, it is guaranteed that after the previous operation the known information does not contain the result of game $i$. 2. `del i` means Xiao D forgets the outcome of game $i$ and removes it from his known information. It is guaranteed that $i$ is an integer with $1 ≤ i ≤ n$, and that after the previous operation the known information contains the result of game $i$.

For each operation, output one real number on a single line: after the operation, under the current known information, the expected total number of games won by Xiao R among the $n$ games.

[Scoring] Your answer is judged correct if its absolute error from the correct answer is within $10^{-4}$. You receive full score only if all your answers are correct; otherwise you receive $0$ points. Please note the output format: output exactly one answer per line, and each answer must be a single real number. The length of each line must not exceed $50$. Wrong output formats will be judged as $0$ points. [Constraints] For $100\%$ of the data, $1 ≤ n ≤ 200000$, $1 ≤ m ≤ 200000$, $0 < p_i, q_i < 1$. For $100\%$ of the data, input values have at most four decimal places. 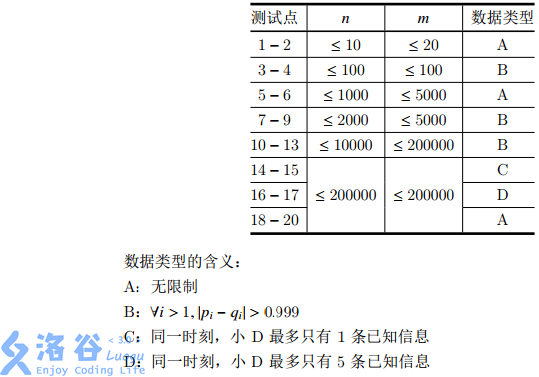There are $20$ test data points in total, each worth $5$ points. The specific assumptions for each test point are shown in the table below:  [Xiao R teaches you math] You may use the following formulas. 1. Conditional probability We write $p(A|B)$ to denote the probability that event $A$ occurs given that event $B$ occurs. Conditional probability can be computed by: $p(A|B)=\frac {p(AB)}{p(B)}$ where $p(AB)$ denotes the probability that both event $B$ and event $A$ occur, and $p(B)$ denotes the probability that event $B$ occurs. 2. Bayes’ formula (Bayes) From conditional probability, we can derive Bayes’ formula: $p(A|B)=\frac {p(B|A)p(A)}{p(B)}$ 3. Law of total probability If a random variable $x$ has $k$ possible values, namely $x_1, x_2,\ldots , x_k$, then $p(A)=\sum^{k}_{i=1} {p(A|x=x_i)p(x=x_i)}$  [Warm reminder] In this problem, if you want to get full score, you may need to consider errors introduced by floating-point arithmetic. Using only addition and multiplication will not introduce large errors, but please be cautious with subtraction and division. 1. Subtracting two numbers that are close in value can introduce very large relative error. 2. If the determinant of a matrix is very small, computing the inverse of that matrix can introduce considerable error. Of course, even if your algorithm is mathematically correct but does not consider floating-point errors, you may still obtain partial scores. Translated by ChatGPT 5