P3774 [CTSC2017] Longest Increasing Subsequence

Zhu Xiaoxia recently studied the longest increasing subsequence (LIS). For an integer sequence $A =(a_1, a_2,\ldots , a_k)$, a subsequence of $A$ is defined as the sequence formed by deleting some elements from $A$ (deleting none or all $k$ elements is allowed) while keeping the remaining elements in their original order. If the elements of this subsequence are strictly increasing from left to right, it is called an increasing subsequence of $A$. Among them, an increasing subsequence with the largest number of elements is called a longest increasing subsequence of $A$. For example, $(2, 4, 5, 6)$ and $(1, 4, 5, 6)$ are both longest increasing subsequences of $(2, 1, 1, 4, 7, 5, 6)$, and their lengths are both $4$. Now Zhu Xiaoxia encounters the following problem: given a sequence $B_m = (b_1, b_2, \ldots, b_m)$, let $C$ be a subsequence of $B_m$. If the length of the LIS of $C$ does not exceed $k$, what is the maximum possible length of $C$? Zhu Xiaoxia thinks this problem is too easy and lacks challenge, so he proposes a harder one. He gives you a sequence $B = (b_1, b_2,\ldots , b_n)$ and several queries. Each query gives two integers $m$ and $k$. For the sequence formed by the first $m$ elements of $B$, namely $B_m = (b_1, b_2, \ldots, b_m)$, and the given $k$, you need to answer the problem above.

The first line contains two integers $n, q$, where $n$ is the length of the sequence $B$, and $q$ is the number of queries. The second line contains $n$ space-separated positive integers $b_1, b_2, \ldots, b_n$. The next $q$ lines follow. The $i$-th line contains two integers $m_i, k_i$, representing a query with $m = m_i$ and $k = k_i$.

Output $q$ lines. For each query, print one integer as the answer, in order.

Sample explanation: Query $1$: For the sequence $(9,6,3,1,5)$, one may choose the subsequence $(9,6,3,1)$, whose LIS length is $1$. Query $2$: For the sequence $(9,6,3,1,5,12,8)$, one may choose the subsequence $(9,6,3,1,12,8)$, whose LIS length is $2$. Query $3$: For the sequence $(9,6,3,1,5,12,8,4,2)$, one may choose the subsequence $(9,6,5,4,2)$, whose LIS length is $1$. Query $4$: For the sequence $(9,6,3,1,5,12,8,4,2)$, one may choose the subsequence $(9,6,3,1,12,8,4,2)$, whose LIS length is $2$. Query $5$: For the sequence $(9,6,3,1,5,12,8,4,2,2,2)$, one may choose the subsequence $(9,6,5,4,2,2,2)$, whose LIS length is $1$. Query $6$: For the sequence $(9,6,3,1,5,12,8,4,2,2,2)$, one may choose the subsequence $(9,6,3,1,5,12,8,4,2,2,2)$, whose LIS length is $3$.  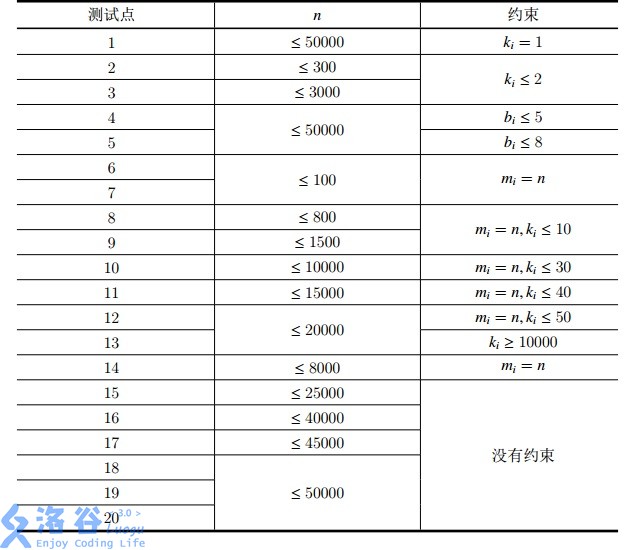Constraints: For $100\%$ of the testdata, $1 \le n \le 5 \times 10^4$, $1 \le b_i \le 5 \times 10^4$, $1 \le q \le 2 \times 10^5$, $1 \le k_i \le m_i \le n$. Translated by ChatGPT 5