P3776 [APIO2017] The Colorful Land

This problem was originally interactive; here it is evaluated in the traditional (non-interactive) format.

In the distant Golden Age, the land of Australia was rectangular and could be divided into a grid with $R$ rows and $C$ columns. Rows are numbered $1$ to $R$ from north to south, and columns are numbered $1$ to $C$ from west to east. The cell $(r, c)$ denotes the land in row $r$ and column $c$. One day, the great Rainbow Serpent started at $(s_r, s_c)$ and moved across Australia. The serpent made $M$ consecutive moves, each time moving one cell to the north (`N`), south (`S`), east (`E`), or west (`W`). Every cell it passed through (including the start and end cells) turned into river. It is guaranteed that the Rainbow Serpent never leaves the $R \times C$ rectangular land at any time. Millions of years later, you want to buy a rectangular area to commemorate the great Rainbow Serpent. You want to color every non-river cell inside the purchased rectangle, with the requirement that adjacent cells must have the same color. Two cells are adjacent if and only if they share a common side. Cells outside your purchased area do not need to be colored. You are given the $M$ movement directions of the Rainbow Serpent and $Q$ candidate rectangular regions to purchase. For each region, determine the maximum number of different colors you can use.

The first line contains four integers $R$, $C$, $M$, and $Q$. The second line contains two integers $s_r$ and $s_c$. The third line contains a string $S$ of $M$ characters, each being one of `N`, `S`, `E`, or `W` (if $M=0$, this line is left blank). Lines $4$ through $Q+3$: each line contains four integers $a_r$, $a_c$, $b_r$, and $b_c$, describing the land you intend to purchase, whose top-left corner is $(a_r, a_c)$ and bottom-right corner is $(b_r, b_c)$.

For each query, output the maximum number of different colors that the land can be painted with.

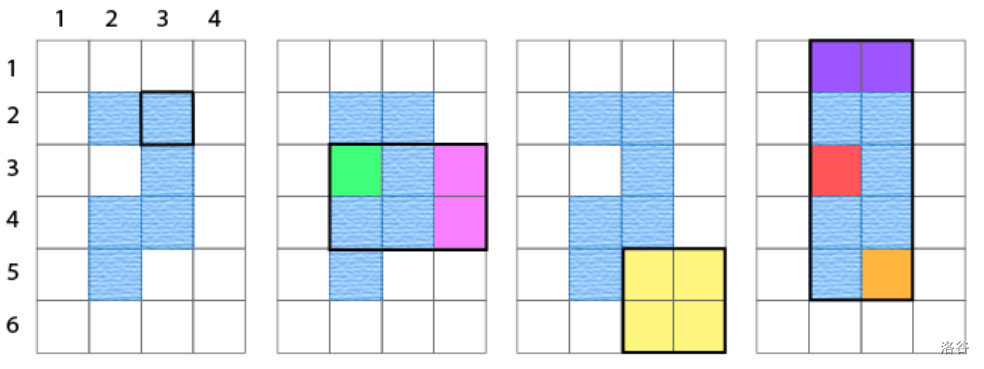
### Sample Explanation The sample corresponds to the figure below, where blue cells represent rivers.  ### Constraints For all testdata, $0 \le M \le 10^5$, and $R, C, Q \ge 1$. For every purchased rectangle, $1 \le a_r \le b_r \le R$ and $1 \le a_c \le b_c \le C$. The detailed subtask scores and additional conditions are as follows. | Subtask ID | Score | $R$ | $C$ | $Q$ | |:-:|:-:|:-:|:-:|:-:| | $1$ | $11$ | $R \le 50$ | $C \le 50$ | $Q \le 1000$ | | $2$ | $12$ | $R = 2$ | $C \le 2 \times 10^5$ | $Q \le 10^5$ | | $3$ | $24$ | $R \le 2 \times 10^5$ | $C \le 2 \times 10^5$ | $Q = 1$ | | $4$ | $27$ | $R \le 1000$ | $C \le 1000$ | $Q \le 10^5$ | | $5$ | $26$ | $R \le 2 \times 10^5$ | $C \le 2 \times 10^5$ | $Q \le 10^5$ | Translated by ChatGPT 5