P3783 [SDOI2017] Genius Hacker

Contestant $\text{SD0062}$, Xiao Q, in order to steal the SDOI7012 problems, infiltrated the SDOI problem setters’ intranet central control system using superb hacking skills. However, besides the central control system, this intranet also assigns a special communication passcode to each directed network cable. A passcode is a string, and different cables may have different passcodes. This looks tricky to Xiao Q, but it cannot stop him. Soon, he analyzed the entire structure of the intranet.

The intranet has $n$ nodes (numbered from $1$ to $n$) and $m$ directed cables. The central control system is at node $1$. Each cable connects an ordered pair of nodes, and starting from node $1$ you can reach any other node by following some cables. Any node can run any application. An application carries a communication passcode. A program can traverse a cable if and only if its current passcode equals the cable’s passcode. Traversing any cable takes some amount of time. Each application can modify its communication passcode at any node. The time to change the passcode itself can be neglected. However, to minimize the amount of modification, you must first call a subroutine to compute the longest common prefix (denote its length by $\mathrm{len}$) between the program’s current passcode and the cable’s passcode. Because obtaining any character of the cable’s passcode is time‑consuming, calling this subroutine once costs $\mathrm{len}$ time units. In addition, Xiao Q found a dictionary in the central control system. Every cable’s passcode is some string from this dictionary. Specifically, this dictionary is a rooted tree with $k$ nodes (numbered from $1$ to $k$), rooted at node $1$. Each edge carries a character. A string $S$ is in the dictionary if and only if there exists a node $u$ such that the characters along the path from the root to $u$ concatenated in order form $S$. Now Xiao Q simultaneously starts $(n-1)$ applications at node $1$. These programs run concurrently without interference. Each program’s initial passcode is empty. He wants to send these programs to the other nodes in the shortest possible time. You need to help Xiao Q compute, for each $i$ ($i=2,3,\dots ,n$), the minimal time for the program destined for node $i$ to finish its task.

The first line contains a positive integer $T$, the number of test cases. For each test case, the first line contains three integers $n, m, k$, the number of intranet nodes, the number of cables, and the number of dictionary tree nodes, respectively. The next $m$ lines each contain four integers $a_i, b_i, c_i, d_i$, meaning that there is a directed cable from node $a_i$ to node $b_i$ whose traversal time is $c_i$, and whose passcode equals the string formed by the characters along the path from the dictionary root to node $d_i$ (which can be empty). Note that the intranet may have self‑loops and multiple edges. The next $(k-1)$ lines each contain three integers $u_i, v_i, w_i$, indicating there is an edge $u_i \rightarrow v_i$ in the dictionary tree whose label is a character $w_i$. It is guaranteed that the given edges form a rooted tree with root $1$, and the labels on the outgoing edges of any node are pairwise distinct.

For each test case, output $(n-1)$ lines. The $i$‑th line is the minimal time for the program to reach node $(i+1)$.

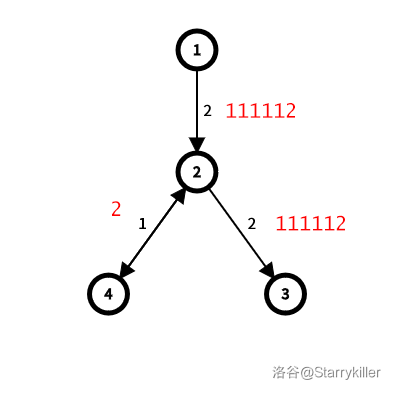
Sample explanation: The following figure shows the intranet structure in the sample. Strings are marked in red.  Let $\mathrm{LCP}(S,T)$ be the length of the longest common prefix of strings $S$ and $T$. For example, $\mathrm{LCP}(\texttt{\textcolor{red}{starry}killer},\texttt{\textcolor{red}{starry}dust})=6$. Let $\epsilon$ be the empty string. One feasible path from $1$ to $3$ is $1 \rightarrow 2 \rightarrow 3$. The required time is $(2 + \mathrm{LCP}(\epsilon , \texttt{1112})) + (2 + \mathrm{LCP}(\texttt{1112} , \texttt{1112})) = 8$. However, this path is not optimal. The optimal path is $1 \rightarrow 2 \rightarrow 4 \rightarrow 2 \rightarrow 3$. | Test point index | $n \le$ | $m \le$ | $k \le$ | Remarks | | :--: | :--: | :--: | :--: | :--: | | $1 \sim 5$ | $5\,000$ | $5\,000$ | $20\,000$ | - | | $6 \sim 14$ | $50\,000$ | $50\,000$ | $20\,000$ | $nk \le 200\,000$ | | $15 \sim 20$ | $50\,000$ | $50\,000$ | $20\,000$ | - | For $100\%$ of the testdata, it is guaranteed that: - $T \leq 10$. - $2 \leq n \leq 50000$, $1 \leq m \leq 50000$, $1 \leq k \leq 20000$. - The number of test cases with $n > 5000$ or $m > 5000$ does not exceed $2$. - $1 \leq a_i, b_i \leq n$, $0 \leq c_i \leq 20000$, $1 \leq d_i \leq k$. - $1 \leq u_i, v_i \leq k$, $1 \leq w_i \leq 20000$. Translated by ChatGPT 5