P3790 文艺数学题

小 Y 在 AK 曼哈顿 OI，CTSC 和 APIO 之后，开始研究数学题。

小 Y 有一张 $N$ 个点，$M$ 条边的无向图（**可能有重边、自环**），每条边都有一个权值 $w$。 你需要计算：所有**生成树的边权的最大公约数**之和，具体操作见样例。 由于答案可能很大，需要**对 $1000000007$ 取模**。

第一行两个正整数 $N,M$，表示点数和边数。 接下来 $M$ 行，每行三个正整数 $u,v,w$，表示一条边连接 $u$ 和 $v$，权值为 $w$。

输出一行一个数，表示答案**对 $1000000007$ 取模**的值。

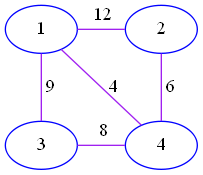
### 样例 $1$ 的解释  显然，这张图有 $8$ 个不同的生成树。 用 $\gcd(x,y,z)$ 表示 $x,y,z$ 的最大公约数，则答案为 $\gcd(12,6,8)+\gcd(6,8,9)+\gcd(8,9,12)+\gcd(9,12,6)+\gcd(9,4,6)+\gcd(12,4,8)+\gcd(12,4,9)+\gcd(6,4,8)$ $=2+1+1+3+1+4+1+2$ $=15$。 ### 数据范围 对于 $20\%$ 的数据，$N\le 10, M\le 20$； 对于另外 $10\%$ 的数据，$N\le 12, M\le 24$； 对于另外 $20\%$ 的数据，$N\le 60, M\le 3000$，且满足$u_i+1=v_i$； 对于另外 $20\%$ 的数据，$N\le 40, M\le 1000, W\le 1000$； 对于另外 $15\%$ 的数据，$N\le 50, M\le 2000$； 对于 $100\%$ 的数据，$N\le 60, M\le 3000, W\le 1000000$。