P3790 Artistic Math Problem

After Xiao Y AK-ed Manhattan OI, CTSC, and APIO, he started studying math problems.

Xiao Y has an undirected graph with $N$ vertices and $M$ edges (**possibly with multiple edges and self-loops**), and each edge has a weight $w$. You need to compute the sum of the greatest common divisors of the edge weights over all spanning trees; see the sample for details. Since the answer may be large, take it **modulo $1000000007$**.

The first line contains two positive integers $N, M$, denoting the number of vertices and the number of edges. The next $M$ lines each contain three positive integers $u, v, w$, denoting an edge connecting $u$ and $v$ with weight $w$.

Output a single integer: the answer **modulo $1000000007$**.

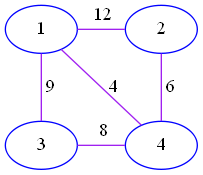
### Explanation of Sample $1$  Obviously, this graph has $8$ different spanning trees. Let $\gcd(x,y,z)$ denote the greatest common divisor of $x, y, z$. Then the answer is $\gcd(12,6,8)+\gcd(6,8,9)+\gcd(8,9,12)+\gcd(9,12,6)+\gcd(9,4,6)+\gcd(12,4,8)+\gcd(12,4,9)+\gcd(6,4,8)$ $=2+1+1+3+1+4+1+2$ $=15$. ### Constraints For $20\%$ of the testdata, $N\le 10, M\le 20$; For another $10\%$ of the testdata, $N\le 12, M\le 24$; For another $20\%$ of the testdata, $N\le 60, M\le 3000$, and it satisfies $u_i+1=v_i$; For another $20\%$ of the testdata, $N\le 40, M\le 1000, W\le 1000$; For another $15\%$ of the testdata, $N\le 50, M\le 2000$; For $100\%$ of the testdata, $N\le 60, M\le 3000, W\le 1000000$. Translated by ChatGPT 5