P3824 [NOI2017] Swimming Pool

Jiulian is a playful girl. Summer vacation has finally arrived. Jiulian decides to invite her friends to go swimming, and she plans to fence off a rectangular sea area outside her private beach as the swimming field. However, the ocean has all kinds of dangers: some places are too deep, and some have poisonous jellyfish. She wants the fenced area to be completely safe.

After preliminary analysis, this sea area can be viewed as a rectangular grid with base length $N$ meters and height $1001$ meters. The base of the grid corresponds to her private beach, and each $1\:\textrm{m} \times 1\:\textrm{m}$ small square represents one unit sea area. She will ask her father to measure tomorrow whether each small square is safe. After obtaining the information, all she needs to do is to fence out her desired swimming field. Her ideal swimming field must satisfy the following three conditions: - Safety. Every unit sea area in the swimming field must be safe. - Rectangular. The swimming field must be an $a \times b$ subgrid of the whole grid. - Adjacent to the beach. The lower boundary of the swimming field must be flush with the bottom boundary of the grid. For example: when $N = 5$, suppose the measurement results are as follows (since $1001$ is too large, only the bottom three rows are shown here; the other parts are unsafe).  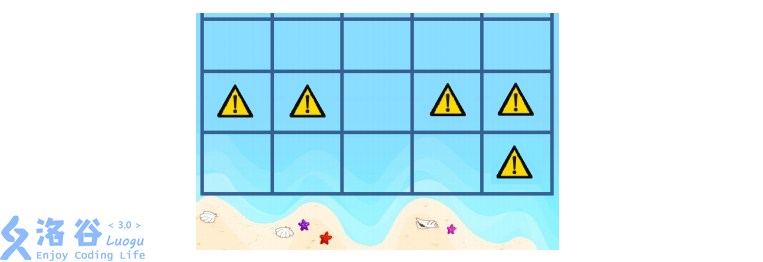Then she can select the $1 \times 4$ subregion in the bottom row, or the $3 \times 1$ subregion in the third column. Note that she cannot select the $1 \times 5$ subregion in the top row because it is not adjacent to the beach. To maximize her friends’ fun, she wants the swimming field to have the largest possible area. Therefore she would choose the $1 \times 4$ subregion in the bottom row as the final plan. Although she will only know tomorrow whether each unit sea area is safe, she wants to estimate now how large the area of her swimming field might be. With a simple estimate, she assumes each unit sea area is independently safe with probability $q$ and unsafe with probability $1 - q$. She wants to know the probability that the maximum area of a selectable swimming field is exactly $K$. However, Jiulian is not interested in mathematics, so she wants you to help her compute this value.

The input contains one line with four positive integers $N, K, x, y$, where $1 \leq x < y < 998\,244\,353$. The value of $q$ is $\dfrac{x}{y}$.

Output one integer: the value of the answer modulo $998\,244\,353$. That is, write the answer as a reduced fraction $\dfrac{a}{b}$ with $\gcd(a, b) = 1$. Output the integer $x$ such that $b x \equiv a \bmod 998\,244\,353$ and $0 \leq x < 998\,244\,353$. It can be proven that such an integer $x$ is unique.

| Test point ID | $N$ | $K$ | |:-:|:-:|:-:| | 1,2 | $= 1$ | $\leq 1000$ | | 3 | $\leq 10$ | $\leq 8$ | | 4 | $\leq 10$ | $\leq 9$ | | 5 | $\leq 10$ | $\leq 10$ | | 6 | $\leq 1000$ | $\leq 7$ | | 7 | $\leq 1000$ | $\leq 8$ | | 8 | $\leq 1000$ | $\leq 9$ | | 9,10,11 | $\leq 1000$ | $\leq 100$ | | 12,13,14 | $\leq 1000$ | $\leq 1000$ | | 15,16 | $\leq 10^9$ | $\leq 10$ | | 17,18 | $\leq 10^9$ | $\leq 100$ | | 19,20 | $\leq 10^9$ | $\leq 1000$ | Translated by ChatGPT 5