[SHOI2012] 信用卡凸包
题目背景
SHOI2012D1T2
题目描述
信用卡是一个矩形，唯四个角作了圆滑处理，使它们都是与矩形的两边相切的 1/4 圆，如下图所示。现在平面上有一些规格相同的信用卡，试求其凸包的周长。注意凸包未必是多边形，因为它可能包含若干段圆弧。
输入输出格式
输入格式
输入的第一行是一个正整数 n，表示信用卡的张数。第二行包含三个实数 a, b, r，分别表示信用卡（圆滑处理前）竖直方向的长度、水平方向的长度，以及 1/4 圆的半径。
之后 n 行，每行包含三个实数 x, y, θ，分别表示一张信用卡中心（即对角线交点）的横、纵坐标，以及绕中心 逆时针旋转的 弧度。
输出格式
输出只有一行，包含一个实数，表示凸包的周长，四舍五入精确到小数点后2 位。
输入输出样例
输入样例 #1
2
6.0 2.0 0.0
0.0 0.0 0.0
2.0 -2.0 1.5707963268输出样例 #1
21.66输入样例 #2
3
6.0 6.0 1.0
4.0 4.0 0.0
0.0 8.0 0.0
0.0 0.0 0.0输出样例 #2
41.60输入样例 #3
3
6.0 6.0 1.0
4.0 4.0 0.1745329252
0.0 8.0 0.3490658504
0.0 0.0 0.5235987756输出样例 #3
41.63说明
样例1说明： 
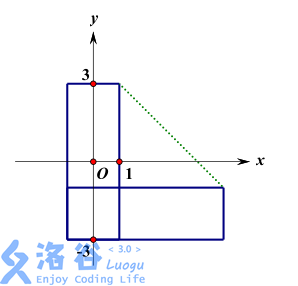
本样例中的 2 张信用卡的轮廓在上图中用实线标出，如果视 1.5707963268为pi/2，那么凸包的周长为16+4sqrt(2)
样例2说明： 
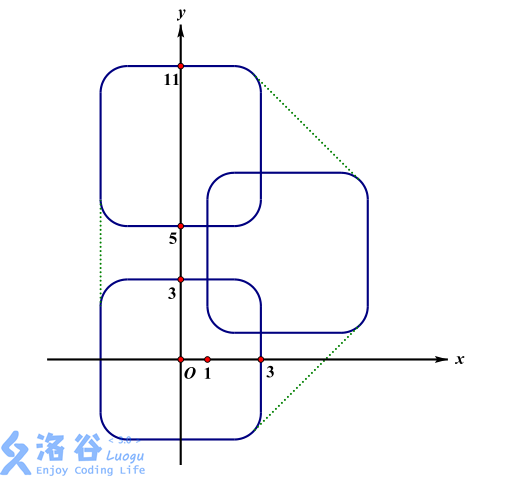
样例3说明： 
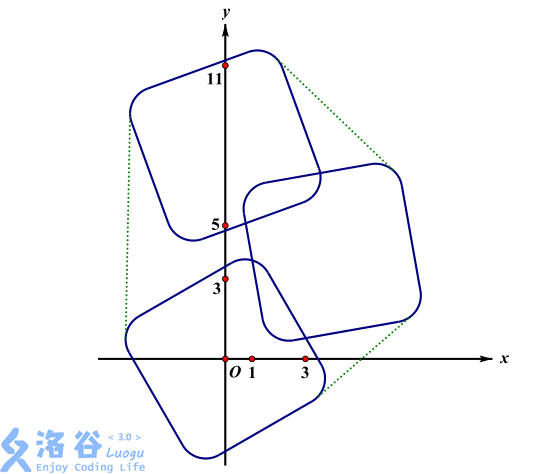
其凸包的周长约为41.628267652。
本题可能需要使用数学库中的三角函数。不熟悉使用方法的选手，可以参考下面的程序及其输出结果：
```cpp
uses math;
const Pi = 3.141592653589793;
begin
writeln(sin(30.0 / 180.0 * Pi) : 0 : 10);
writeln(cos(60.0 / 180.0 * Pi) : 0 : 10);
writeln(tan(45.0 / 180.0 * Pi) : 0 : 10);
writeln(arcsin(1.0) : 0 : 10);
writeln(arccos(0.0) : 0 : 10);
writeln(arctan(1.0) : 0 : 10);
end.
```
```cpp
#include <iostream>
#include <math.h>
using namespace std;
const double Pi = 3.141592653589793;
int main()
{
cout.setf(ios::fixed);
cout.precision(10);
cout<<sin(30.0 / 180.0 * Pi)<<endl;
cout<<cos(60.0 / 180.0 * Pi)<<endl;
cout<<tan(45.0 / 180.0 * Pi)<<endl;
cout<<asin(1.0)<<endl;
cout<<acos(0.0)<<endl;
cout<<atan(1.0)<<endl;
return 0;
}
```
输出结果：0.5000000000
0.5000000000
1.0000000000
1.5707963268
1.5707963268
0.7853981634
数据范围：
