P3829 [SHOI2012] Credit Card Convex Hull
Background
SHOI2012D1T2
Description
A credit card is a rectangle whose four corners are rounded so that each corner is a $1/4$ circle tangent to the two adjacent sides, as shown below. Now there are several credit cards of identical specifications placed on the plane. Find the perimeter of their convex hull. Note that the convex hull is not necessarily a polygon, because it may contain several circular arcs.

Input Format
The first line contains a positive integer $n$, the number of credit cards. The second line contains three real numbers $a$, $b$, $r$, which denote, respectively, the length of the credit card (before rounding) in the vertical direction, the length in the horizontal direction, and the radius of each $1/4$ circle.
Then there are $n$ lines. Each line contains three real numbers $x$, $y$, $\theta$, which denote, respectively, the $x$- and $y$-coordinates of a card’s center (i.e., the intersection point of its diagonals), and the angle (in radians) it is rotated counterclockwise about its center.
Output Format
Output a single line containing one real number: the perimeter of the convex hull, rounded to 2 decimal places.
Explanation/Hint
Explanation for Sample 1: 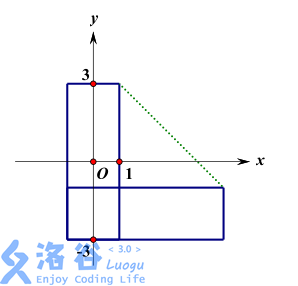
In this sample, the outlines of the 2 credit cards are drawn in solid lines above. If we regard $1.5707963268$ as $\pi/2$, then the perimeter of the convex hull is $16 + 4\sqrt{2}$.
Explanation for Sample 2: 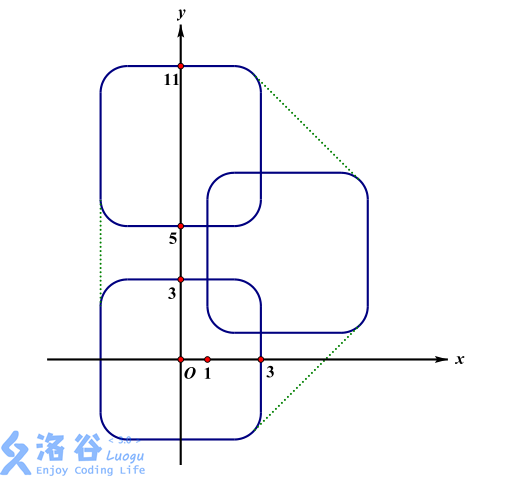
Explanation for Sample 3: 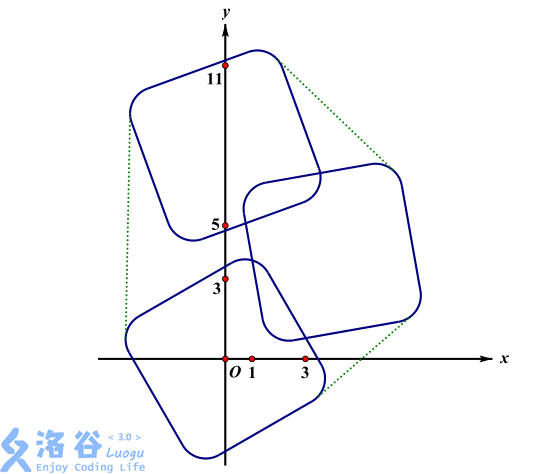
The perimeter of its convex hull is approximately $41.628267652$.
This problem may require trigonometric functions from the math library. If you are not familiar with their usage, you can refer to the following programs and their outputs:
```cpp
uses math;
const Pi = 3.141592653589793;
begin
writeln(sin(30.0 / 180.0 * Pi) : 0 : 10);
writeln(cos(60.0 / 180.0 * Pi) : 0 : 10);
writeln(tan(45.0 / 180.0 * Pi) : 0 : 10);
writeln(arcsin(1.0) : 0 : 10);
writeln(arccos(0.0) : 0 : 10);
writeln(arctan(1.0) : 0 : 10);
end.
```
```cpp
#include
#include
using namespace std;
const double Pi = 3.141592653589793;
int main()
{
cout.setf(ios::fixed);
cout.precision(10);
cout