P3830 [SHOI2012] Random Tree

SHOI2012 D1T3.

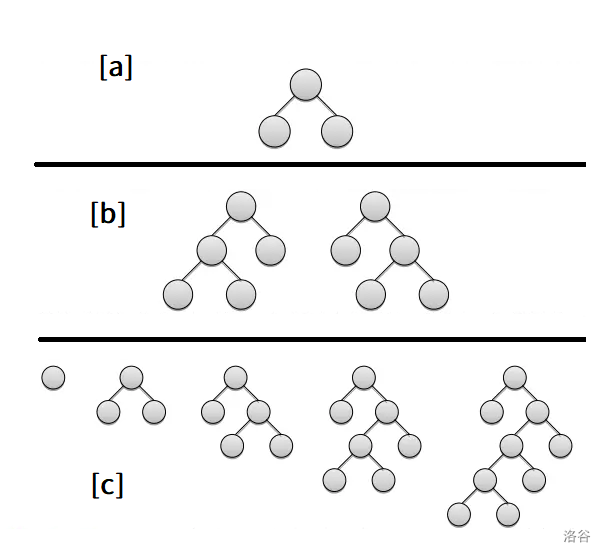
A binary tree with $n$ leaf nodes can be generated as follows. Initially there is only the root node. First, expand the root node (in this problem, “expand” means adding left and right children to a leaf node): [a] Then, uniformly at random choose one of the two leaf nodes to expand, i.e., generate one of the following two trees: [b] After that, at each step, uniformly at random choose one leaf node from all current leaf nodes and expand it. Repeat this operation until there are $n$ leaf nodes. For example, a binary tree with $5$ leaf nodes might be generated by the following steps. [c] For a binary tree with $n$ leaf nodes generated by this process, find: 1. The expected value of the average depth of the leaf nodes. 2. The expected value of the tree depth. The root node is defined to have depth $0$. 

The input contains one line with two positive integers $q$, $n$, representing the query type and the number of leaf nodes, respectively.

Output one line with a real number $d$, rounded to $6$ digits after the decimal point. If $q = 1$, then $d$ is the expected value of the average depth of the leaf nodes; if $q = 2$, then $d$ is the expected value of the tree depth.

【Explanation for Samples 1 and 2】 The expected value of a random variable is the sum of each value times its probability. Let the possible values of random variable $X$ be $x_1, x_2, \cdots, x_n$, and their probabilities be $p_1, p_2, \cdots, p_n$. Then the expected value of $X$ is $E(X)=\sum_{i = 1}^{n} p_i x_i$. For example, when rolling a fair die labeled with the $6$ numbers $1, 2, 3, 4, 5, 6$, the expected value of the outcome is: $E=\frac{1}{6}\times 1+\frac{1}{6}\times 2+\frac{1}{6}\times 3+\frac{1}{6}\times 4+\frac{1}{6}\times 5+\frac{1}{6}\times 6 = 3.5$, even though $3.5$ is not one of the die faces. As another example, consider a single-choice question with $4$ options: a correct answer gives $5$ points, no answer gives $0$ points, and a wrong answer gives $-1$ point. If we do not answer, we certainly get $0$; if we guess uniformly at random, the expected score is: $E=\frac{1}{4}\times 5+\frac{1}{4}\times (-1)+\frac{1}{4}\times (-1)+\frac{1}{4}\times (-1)=\frac{1}{2}$. 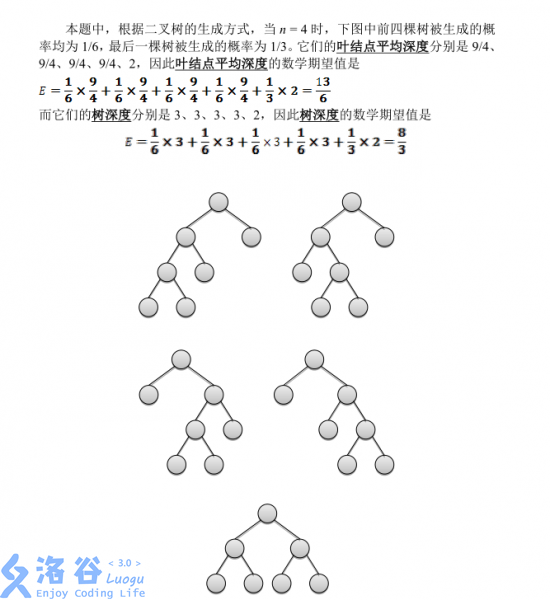In this problem, according to the generation process, when $n = 4$, in the figure below the first four trees are generated with probability $1/6$ each, and the last tree with probability $1/3$. Their average leaf depths are $9/4$, $9/4$, $9/4$, $9/4$, $2$, so the expected value of the average leaf depth is $E=\frac{1}{6}\times \frac{9}{4}+\frac{1}{6}\times \frac{9}{4}+\frac{1}{6}\times \frac{9}{4}+\frac{1}{6}\times \frac{9}{4}+\frac{1}{3}\times 2=\frac{13}{6}$. Their tree depths are $3, 3, 3, 3, 2$, so the expected value of the tree depth is $E=\frac{1}{6}\times 3+\frac{1}{6}\times 3+\frac{1}{6}\times 3+\frac{1}{6}\times 3+\frac{1}{3}\times 2=\frac{8}{3}$. Constraints | Testdata ID | $q$ | $n$ | | ---- | ---- | ---- | | 1, 2 | $q = 1$ | $2 \leq n \leq 10$ | | 3, 4, 5 | $q = 1$ | $2 \leq n \leq 100$ | | 6, 7 | $q = 2$ | $2 \leq n \leq 10$ | | 8, 9, 10 | $q = 2$ | $2 \leq n \leq 100$ |    Translated by ChatGPT 5