P3831 [SHOI2012] The Way Home

SHOI2012 D2T1.

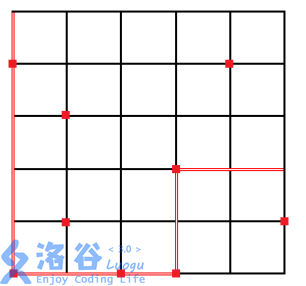
In 2046, the urban rail transit construction of OI City was finally completed. Thanks to meticulous planning, the completed rail network consists of $2n$ subway lines, forming a grid with $n$ vertical and $n$ horizontal lines. As shown in the figure below, each of these $2n$ lines contains $n$ stations, and each station lies at the intersection of one vertical line and one horizontal line. For cost reasons, not every station allows in-station transfers. There are $m$ stations where in-station transfer is possible; in the figure below, stations marked with squares are transfer stations. It is known that traveling one stop takes $2$ minutes, and an in-station transfer requires $1$ minute of walking. Serenade wants to know, without exiting the station mid-journey, the minimum time needed to get home from school (waiting time is ignored). 

The first line contains two integers $n, m$. Each of the next $m$ lines contains two integers $x, y$, indicating that the intersection of the $x$-th horizontal line and the $y$-th vertical line is an in-station transfer station. The next line contains four integers $x_1, y_1, x_2, y_2$. They mean that Serenade boards at the intersection of the $x_1$-th horizontal line and the $y_1$-th vertical line, and alights at the intersection of the $x_2$-th horizontal line and the $y_2$-th vertical line.

Output one line: the minimum time for Serenade to get home with an optimal choice of lines. If Serenade cannot get home without exiting the station to transfer, output `-1`.

- For $30\%$ of the testdata, $n \le 50, m \le 1000$. - For $60\%$ of the testdata, $n \le 500, m \le 2000$. - For $100\%$ of the testdata, $n \le 20000, m \le 100000$. Translated by ChatGPT 5