[IOI2017] Toy Train

# 滥用本题评测将被封号 ### 由于技术限制，请不要使用 C++ 14 (GCC 9) 提交本题。 这是一道交互题，你只需要实现代码中要求的函数。 你的代码不需要引用任何额外的头文件，也不需要实现 `main` 函数。

Arezou 和她的兄弟 Borzou 是双胞胎。他们收到的生日礼物是一套好玩的玩具火车。他们用它建了一下 $n$ 个车站和 $m$ 段单向轨道的铁路系统。这些车站的编号是从 $0$ 到 $n-1$。每段轨道都始于某一车站，然后终于同一车站或其他车站。每个车站至少会有一段轨道以它为起点。 其中有些车站是充电车站。无论何时，如果火车抵达某个充电车站。无论何时，如果火车抵达某个充电车站，它都会被充到满电。满电火车拥有足够的动力连续地试过 $n$ 段轨道，但是如果不再充电的话，在即将进入第 $n+1$ 段轨道时它就会因电已用光而停车。 每个车站都有一个轨道开关，可以扳向任一以该车站为起点的轨道。火车从某个车站驶出时，驶向的正是该车站的开关所扳向的轨道。 这对双胞胎打算用他们的火车玩个游戏。他们已经分完了所有的车站：每个车站要么归 Arezou，要么归 Borzou。游戏里面只有一列火车。游戏开始时，这列火车停在车站 $s$ ，并且充满了电。为启动游戏，车站 $s$ 的拥有者把车站 $s$ 的开关扳向某个以 $s$ 为起点的轨道。随后他们启动火车，火车也就开始沿着轨道行驶。无论何时，在火车首次进入某一车站时，该车站的拥有者都要扳定车站开关。开关一旦扳定，它就会保持状态不变直到游戏结束。因此，火车如果开到了一个曾经进过的车站，就会沿着与之前相同的轨道开出该车站。 由于车站数量是有限的，火车的行驶最终都会落入某个环路。环路是指一系列**不同**的车站 $c_0,c_1,\cdots ,c_{k-1}$，其中火车在离开车站 $c_i\ \ (0\leqslant i < k-1)$ 后驶上连向车站 $c_{i+1}$ 的轨道，在离开车站 $c_{k-1}$ 后驶上连向车站 $c_0$ 的轨道。一个环路可能只包括一个车站（此时 $k=1$），即火车从车站 $c_0$ 驶出后又驶上了连向车站 $c_0$ 的轨道。 如果火车能够连续行驶跑完，Arezou 就赢了。否则火车最后会把电用光而停车，这样 Borzou 就赢了。换句话说，如果 $c_0,c_1,\cdots ,c_{k-1}$中至少有一个充电车站，且使得火车能够不断地充电而沿着环路跑个没完，Arezou 赢。否则，它就会最终把电用光（有可能是在沿着环路跑好几圈后），Borzou 赢。 现在给你一个这样的铁路系统。Arezou 和 Borzou将会玩 $n$ 轮游戏。其中在第 $s$ 轮游戏中（$0\leqslant s \leqslant n-1$），火车最初停在车站 $s$ 上。你的任务是，对每一轮游戏，判断是否无论 Borzou 怎么玩，Arezou 都必胜。 ## 实现细节 你需要实现下面的函数 (C++) `std::vector who_wins(std::vector<int> a, std::vector<int> r, std::vector<int> u, std::vector<int> v)` (Java) `int[] who_wins(int[] a, int[] r, int[] u, int[] v)` - $a$：长度为 $n$ 的数组。如果 Arezou 拥有车站 $i$，则 $a_i=1$；否则 Borzou 拥有车站 $i$，且 $a_i=0$。 - $r$：长度为$n$的数组。如果车站$i$是充电车站，则$r[i]=1$。否则$r[i]=0$。 - $u$ 和 $v$：长度为 $m$ 的数组。对于所有 $0\leqslant i \leqslant m-1$，存在某一单向轨道，其起点为 $u_i$，终点为 $v_i$。 - 该函数需要返回一个长度为 $n$ 的数组 $w$。对于每个 $0\leqslant i \leqslant n-1$，如果在火车最初停在车站 $i$ 的游戏中，不管 Borzou 怎么玩，Arezou 都能赢，则 $w_i$ 的值应为 $1$。否则 $w_i$ 的值应为 $0$。

你需要实现上述子程序。

你的子程序需要返回一个合法的结果。

a = [0, 1]
r = [1, 0]
u = [0, 0, 1, 1]
v = [0, 1, 0, 1]

who_wins = [1, 1]

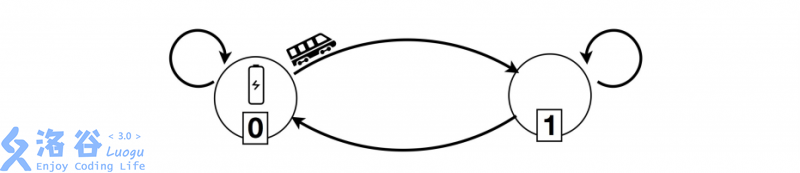
 - 这里有 $2$ 个车站。Borzou 拥有充电车站 $1$。Arezou拥有充电车站 $1$，但是它不是充电车站。 - 这里有 $4$ 段轨道 $(0,0),(0,1),(1,0)$ 和 $(1,1)$，其中 $(i,j)$ 表示一个以车站 $i$ 为起点、车站$j$为终点的单向轨道。 - 考虑火车最初停在车站 $0$ 的游戏。如果 Borzou 将车站 $0$ 的开关扳向轨道 $(0,0)$，那么火车就会沿着这个环形轨道绕个没完（注意，车站 $0$ 是一个充电车站）。在这种情况下，Arezou 赢。否则，如果 Borzou 把车站 $0$ 的开关扳向轨道 $(0,1)$，Arezou 可以把车站 $1$ 的开关扳向轨道 $(1,0)$。这样的话，火车将会在两个车站之间绕个不停。Arezou 还是会赢，因为车站$0$是充电车站，火车将跑个没完。因此，无论 Borzou 怎么玩，Arezou 都会赢。 - 根据类似的逻辑，在火车最初停在车站 $1$ 的游戏中，无论 Borzou 怎么玩，Arezou 也都会赢。因此，函数应当返回 $[1,1]$。 ## 数据范围和限制 - $1\leqslant n \leqslant 5000$ - $n \leqslant m \leqslant 20000$ - 至少会有一个充电车站。 - 每个车站至少会有一段轨道以它为起点。 - 可能会有某个轨道的起点和终点是相同的（即 $u_i=v_i$）。 - 所有轨道两两不同。也就是说，不存在这样的两个下标 $i$ 和 $j$（$0\leqslant i < j \leqslant m-1$），使得 $u_i=u_j$ 且 $v_i=v_j$。 - 对于所有 $0\leqslant i \leqslant m-1$，都有 $0\leqslant u_i,v_i \leqslant n-1$。 ## 子任务 1. ($5$ 分) 对于所有 $0 \leqslant i \leqslant m-1$，都有 $v_i=u_i$ 或者 $v_i=u_i+1$。 2. ($10$ 分) $n\leqslant 15$。 3. ($11$ 分) Arezou 拥有所有车站。 4. ($11$ 分) Borzou 拥有所有车站。 5. ($12$ 分) 充电车站的数量为 $1$。 6. ($51$ 分) 无任何限制。