P3840 [IOI 2017] Simurgh

This problem temporarily does not support submissions. Time limit: 3 s, memory limit: 1024 MB.

According to the ancient Persian legend from the Shahnameh, Zal, a legendary Persian hero, falls madly in love with Rudaba, the princess of the kingdom of Kabul. When Zal proposes to Rudaba, her father gives him a challenge. There are $n$ cities in Persia, labeled from $0$ to $n - 1$, and $m$ bidirectional roads, labeled from $0$ to $m - 1$. Each road connects two different cities. At most one road connects any pair of cities. Some roads are royal roads, reserved for the royal family, but this is secret. Zal’s task is to find which roads are royal. Zal has a map of Persia that includes all cities and all roads. He does not know which roads are royal, but he can ask for help from the Simurgh—the benevolent mythical bird and Zal’s protector. However, the Simurgh does not want to tell him directly which roads are royal. Instead, the Simurgh tells Zal that the set of all royal roads is a golden set. A set of roads is a golden set if and only if: - It contains exactly $n - 1$ roads, and - For every pair of cities, it is possible to travel from one to the other using only roads from this set. Additionally, Zal can ask the Simurgh some questions. For each question: 1. Zal selects a golden set of roads, then 2. The Simurgh tells Zal how many roads in the selected golden set are royal. Your program may ask the Simurgh at most $q$ questions to help Zal find the set of royal roads. The grader will play the role of the Simurgh. Implementation details You need to implement the following function: ```cpp int[] find_roads(int n, int[] u, int[] v) ``` - $n$: the number of cities. - $u$ and $v$: arrays of length $m$. For all $0 \le i \le m - 1$, $u[i]$ and $v[i]$ are the cities connected by road $i$. - The function must return an array of length $n - 1$ containing the labels of all royal roads (in any order). Your program may call the following function from the grader at most $q$ times: ```cpp int count_common_roads(int[] r) ``` - $r$: an array of length $n - 1$ containing the labels of a golden set of roads (in any order). - The function returns the number of royal roads contained in $r$.

无

无

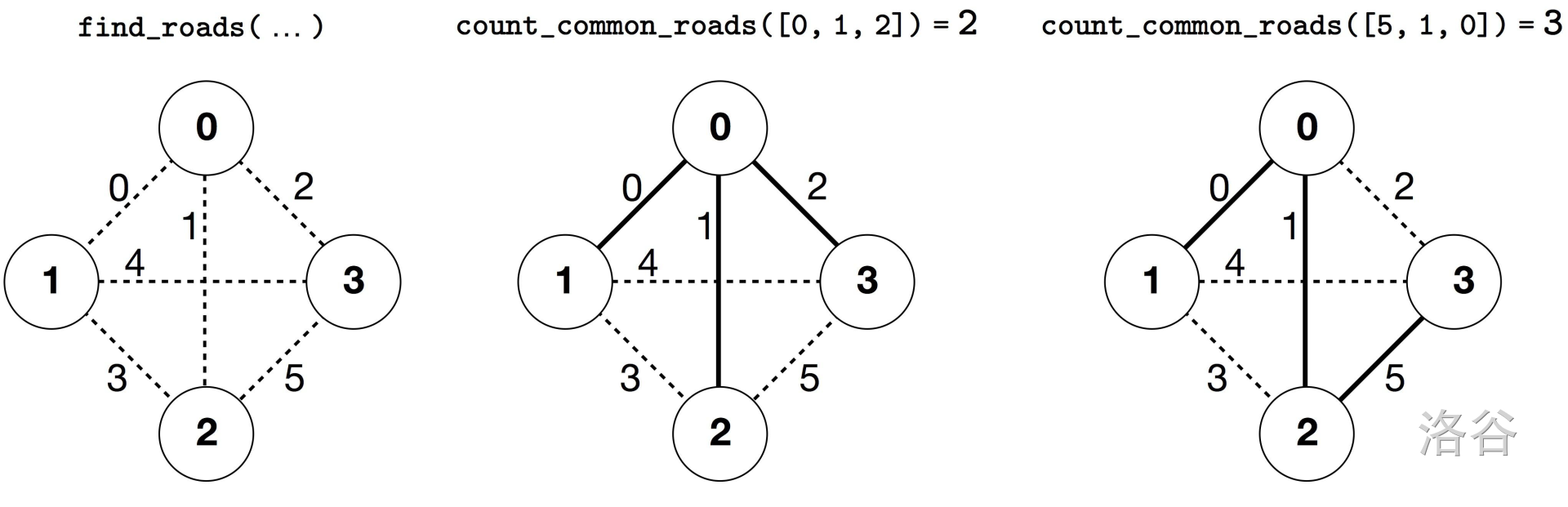
Example ``` find_roads(4, [0, 0, 0, 1, 1, 2], [1, 2, 3, 2, 3, 3]) ```  In this example there are $4$ cities and $6$ roads. We denote by $(a, b)$ the road connecting cities $a$ and $b$. The roads are labeled from $0$ to $5$ in the following order: $(0, 1)$, $(0, 2)$, $(0, 3)$, $(1, 2)$, $(1, 3)$, and $(2, 3)$. Each golden set contains $n - 1 = 3$ roads. Suppose the royal roads are those with labels $0$, $1$, and $5$, i.e., $(0, 1)$, $(0, 2)$, and $(2, 3)$. Then: - `count_common_roads([0, 1, 2])` returns $2$. This query uses roads $0$, $1$, and $2$, i.e., $(0, 1)$, $(0, 2)$, and $(0, 3)$. Among them, two roads are royal. - `count_common_roads([5, 1, 0])` returns $3$. This query uses all royal roads. The function `find_roads` must return `[5, 1, 0]` or any other array of length $3$ containing these three elements. Note that the following calls are not allowed: - `count_common_roads([0, 1])`: here the length of $r$ is not $3$. - `count_common_roads([0, 1, 3])`: here $r$ is not a golden set, because it is impossible to travel from city $0$ to city $3$ using only the roads $(0, 1)$, $(0, 2)$, and $(1, 2)$. Constraints - $2 \le n \le 500$. - $n - 1 \le m \le n(n - 1) / 2$. - $0 \le u[i], v[i] \le n - 1$ (for all $0 \le i \le m - 1$). - For all $0 \le i \le m - 1$, road $i$ connects two different cities (i.e., $u[i] \neq v[i]$). - There is at most one road between every pair of cities. - It is possible to travel between any pair of cities using these roads. - All royal roads form a golden set. - `find_roads` may call `count_common_roads` at most $q$ times. In each call, the roads given by $r$ must form a golden set. Subtasks 1. (13 points) $n \le 7$, $q = 30000$. 2. (17 points) $n \le 50$, $q = 30000$. 3. (21 points) $n \le 240$, $q = 30000$. 4. (19 points) $q = 12000$, every pair of cities is connected by a road. 5. (30 points) $q = 8000$. Sample grader The sample grader reads input in the following format: - Line $1$: $n\ m$. - Line $2 + i$ (for all $0 \le i \le m - 1$): $u[i]\ v[i]$. - Line $2 + m$: $s[0]\ s[1]\ \dots\ s[n - 2]$. Here $s[0], s[1], \dots, s[n - 2]$ are the labels of all royal roads. If `find_roads` calls `count_common_roads` at most $30000$ times and correctly returns the set of royal roads, the sample grader outputs `YES`. Otherwise the sample grader outputs `NO`. Note that in the sample grader the function `count_common_roads` does not check whether $r$ satisfies all conditions of a golden set. Instead, it simply counts how many elements of $r$ are royal and returns that number. However, in your submission, if you call `count_common_roads` with a set of labels that does not correspond to a golden set, the verdict will be 'Wrong Answer'. Technical tip For efficiency reasons, in C++ and Pascal the function `count_common_roads` uses call by reference. You can call this function as usual. The grader guarantees that it will not modify the values in $r$. Translated by ChatGPT 5