P3841 [IOI 2017] Ancient Books

**[Submission not supported].**

The city of Tehran is home to the National Library of Iran. Its crown jewels are displayed in a long hall with $n$ tables arranged in a row, numbered from $0$ to $n-1$ from left to right. Each table displays a handwritten ancient book. The books are ordered by their historical year, which makes it hard for visitors to find them by title. Therefore, the head of the library decides to rearrange them in alphabetical order by title. The librarian Aryan will do this task. He creates a list $p$ of length $n$, consisting of distinct integers from $0$ to $n-1$. This list describes the rearrangement in alphabetical order: for $0 \leq i < n$, the book currently on table $i$ should be moved to table $p[i]$. Aryan starts the rearrangement at table $s$. He wants to return to the same table after finishing the job. Because the books are extremely valuable, at any time he must not hold more than one book. During the rearrangement, Aryan performs a sequence of operations. Each operation must be one of the following: - If he is not holding a book and there is exactly one book on his current table, he may pick up this book. - If he is holding a book and there is exactly one book on his current table, he may swap the book in his hand with the book on the table. - If he is holding a book and there is no book on his current table, he may put the book down on the table. - He may walk to any table. He may carry a book while walking. For all $0 \leq i, j \leq n-1$, the distance between tables $i$ and $j$ is exactly $|j - i|$ meters. Your task is to compute the minimum possible total distance Aryan walks to complete the rearrangement.

C++ only. You need to implement the following function: ```cpp long long minimum_walk(std::vector p, int s) ``` $p$ is an array of length $n$. Initially, the book on table $i$ must be moved by Aryan to table $p[i]$ (for all $0 \leq i < n$). $s$ is the index of the table where Aryan starts, and it is also where he must end after completing the rearrangement. The function should return the minimum total walking distance (in meters) required for Aryan to complete the rearrangement.

Your function should return the minimum total walking distance (in meters).

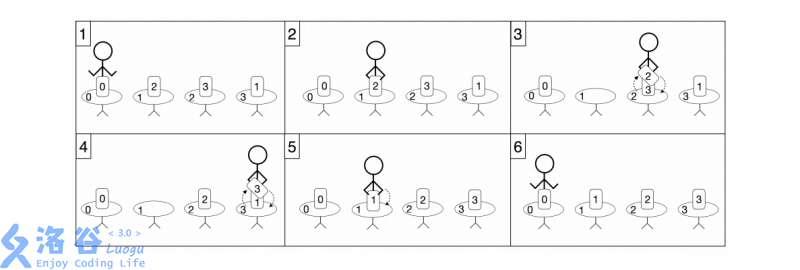
The judge calls `minimum_walk([0, 2, 3, 1], 0)`.  In this example, $n = 4$, and initially Aryan is at table $0$. He proceeds as follows: - Walk to table $1$ and pick up the book there. This book should be placed on table $2$. - Then walk to table $2$ and swap the book in his hand with the book on the table. The new book in his hand should be placed on table $3$. - Then walk to table $3$ and swap the book in his hand with the book on the table. The new book in his hand should be placed on table $1$. - Then walk to table $1$ and put the book in his hand onto the table. - Finally, return to table $0$. Note that the book on table $0$ is already in the correct position, i.e., table $0$, so Aryan does not need to pick it up. In this plan, his total walking distance is $6$ meters. This is optimal; therefore, the function should return $6$. ### Constraints - $1 \leq n \leq 1\ 000\ 000$. - $0 \leq s \leq n - 1$. - The array $p$ contains $n$ distinct integers from $0$ to $n - 1$ (inclusive). ### Subtasks 1. (12 points) $n \leq 4$ and $s = 0$. 2. (10 points) $n \leq 1000$ and $s = 0$. 3. (28 points) $s = 0$. 4. (20 points) $n < 1000$. 5. (30 points) No additional constraints. Translated by ChatGPT 5