P3852 [TJOI2007] Children

There are $N$ children in a kindergarten. The teacher wants to select some of them to play a "drop the handkerchief" game. However, the teacher did not expect that even among such young children, some pairs have conflicts. The teacher wants to include as many children as possible in the game, but he is troubled because he does not want any two selected children to have a conflict. Given $M$ pairs of conflicts among the children, can you help the teacher compute the maximum number of children he can select for this game?

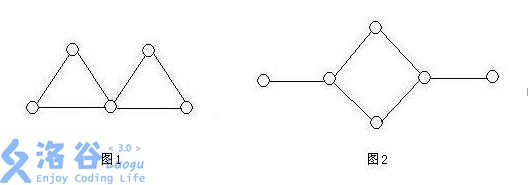
Explanation of the conflict constraint: If we regard any two conflicting children as two adjacent vertices in an undirected graph, the testdata guarantees that the graph formed by the $M$ conflicting pairs contains no cycle with more than 3 vertices. (Figure 1 satisfies the requirement, while Figure 2 does not.) 

The first line contains two integers $N$ and $M$ separated by a space, indicating there are $N$ children and $M$ pairs of conflicts. Each of the next $M$ lines contains two integers $a$ and $b$ (separated by a space), meaning that child $a$ and child $b$ have a conflict. (Children are numbered starting from $1$.)

Output one line containing a single integer — the maximum number of children the teacher can select to play the game.

There are 6 children. The conflicts contain a cycle $1 - 2 - 3$ and another cycle $3 - 4 - 5$. Therefore, you can select exactly one child from each of these two cycles, and child $3$ cannot be selected. Constraints: - For $20\%$ of the testdata, $1 \le N \le 20$. - For $40\%$ of the testdata, $1 \le N \le 50$. - For $100\%$ of the testdata, $1 \le N \le 200$. - All $100\%$ of the testdata satisfy the conflict constraint described in the problem. Translated by ChatGPT 5