P3860 [TJOI2009] Martian's Mobile Phone
Background
At the invitation of the Martians, you are to design a new type of phone for them. We know that a standard Earth phone has $10$ numeric keys, the $26$ letters `a`…`z` are each associated with some numeric key, and the letters on any single numeric key must form a contiguous segment of the alphabet. For example, the figure below shows a standard scheme for an Earth phone:
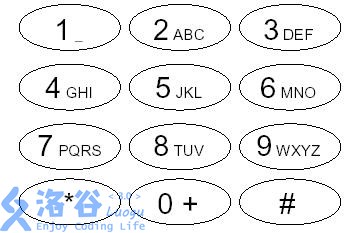
Description
To input a letter, we must press its numeric key several times consecutively; the number of presses equals the letter’s position on that key. For example, in the scheme above, to input `C`, we press numeric key `2` three times; to input `M`, we press numeric key `6` once.
The Martian phone is similar to the Earth phone: it has $M$ Martian numeric keys, and you need to place the $N$ letters of the Martian alphabet onto these $M$ keys. (Likewise, the letters on any single numeric key must be a contiguous block of Martian letters.) Now, given the occurrence count of each letter in a passage of Martian text, your design must minimize the total number of key presses required to input this passage.
Input Format
The first line of input contains two numbers, $N$ and $M$, the number of Martian letters and the number of keys on the Martian phone, respectively. The next $N$ lines each contain one number, in order, giving the occurrence count of each letter in the passage. Each count does not exceed $1000$.
Output Format
The first line of output contains a single number, the minimum total number of key presses.
The next $M$ lines describe one design: each line contains a number, in order, indicating how many Martian letters are placed on each numeric key. (These numbers may be $0$.)
If multiple designs achieve the same minimum, output the one with the fewest letters on the first numeric key; if still tied, among those choose the one with the fewest letters on the second numeric key; and so on.
Explanation/Hint
### Constraints
For $100\%$ of the data, $1 \le N \le 500$, $1 \le M \le 100$.
Translated by ChatGPT 5