P3884 [JLOI2009] Binary Tree Problem

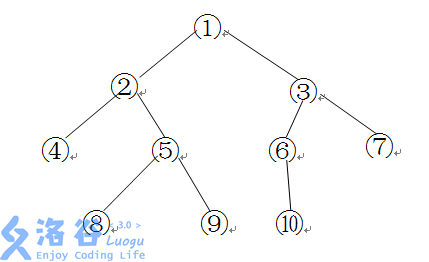
For the binary tree shown below, its depth, width, and distances between nodes are as follows: - Depth: $4$. - Width: $4$. - The distance between nodes 8 and 6: $8$. - The distance between nodes 7 and 6: $3$. Here, the width is the maximum number of nodes on the same level of the binary tree. The distance between nodes $u$ and $v$ is defined as twice the number of edges directed toward the root plus the number of edges directed toward the leaves, along the shortest directed path from $u$ to $v$.  Given a binary tree rooted at node 1, compute its depth, width, and the distance between two specified nodes $x, y$.

The first line contains an integer $n$, the number of nodes in the tree. The next $n - 1$ lines each contain two integers $u, v$, indicating that there is an edge connecting $u$ and $v$ in the tree. The last line contains two integers $x, y$, asking for the distance between $x$ and $y$.

Output three lines, each containing one integer, representing the depth, the width, and the distance between $x$ and $y$, in this order.

For all test points, $1 \leq u, v, x, y \leq n \leq 100$, and the input describes a tree. It is guaranteed that $u$ is the parent of $v$. Translated by ChatGPT 5