P3893 [GDOI2014] Beyond

Jodie slowly walks into the laboratory. The spirit Aiden, who follows by her side, seems a bit upset, but still sticks closely to Jodie. Today’s experiment takes place on a very large circular ring with $L$ cells. Each cell displays a lowercase English letter. Jodie starts from any cell. Whenever she leaves a cell, the letter in that cell changes randomly; no one knows what it will become. Jodie walks clockwise around the ring without ever turning back. Each time she enters a cell, she writes down the letter currently displayed in that cell. Since Jodie cannot turn back and does not know how many cells the ring has, she does not know when she will reach a cell she has already visited. So she asks Aiden to remind her when her next step would enter a previously visited cell. However, after a quarrel, Aiden gets angry and decides to tell her only after Jodie has already stepped into $K$ repeated cells (with $K \geq 0$). Jodie performs two experiments and records the two paths. Before the second experiment begins, the letter in each cell is reset to the state it had before the first experiment started. Jodie discovers Aiden’s prank, so she can only report the largest possible $L$ to the experimenters. To help you better understand the problem, please analyze the example: Suppose $L = 4$, $K = 1$. 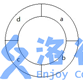Before the first experiment starts, the letters displayed by each cell are as shown below:  Jodie starts walking from the cell showing the letter `a`. Aiden tells her to stop after she has stepped into $K$ repeated cells, so Jodie takes a total of $5$ steps. 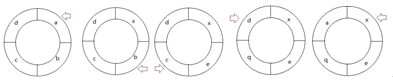After each step, the cells change as follows (the arrow points to the cell where Jodie is):  Jodie’s second experiment starts from the cell showing the letter `c`. After each step, the cells change as follows (the arrow points to the cell where Jodie is):  The two paths recorded by Jodie are: `abcdx` `cdabz` Now you are given the length $N$ of each of Jodie’s two recorded paths, and the two strings she wrote down, but $K$ is unknown. Please find the maximum possible value of $L$.

The first line contains an integer $N$. The second line contains a string of length $N$, consisting only of lowercase letters. The third line contains a string of length $N$, consisting only of lowercase letters.

Output a single number $L$, the maximum possible number of cells on the ring.

Constraints: - For $20\%$ of the testdata, $1 \leq N \leq 5{,}000$. - For $50\%$ of the testdata, $1 \leq N \leq 600{,}000$. - For $100\%$ of the testdata, $1 \leq N \leq 2{,}000{,}000$. Translated by ChatGPT 5