P3894 [GDOI2014] Teleportation

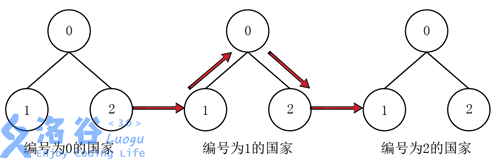
There are $n$ countries, numbered from $0$ to $n-1$. The $i$-th country contains $m_i$ cities, numbered from $0$ to $m_{i}-1$, where the city numbered $0$ is the capital. For convenience, we use $(i,j)$ to denote the $j$-th city of the $i$-th country. The cities within the same country are connected by roads that form a tree, with the capital as the root. There are no roads between cities of different countries; you can only travel via teleportation portals. In each country, only cities that are leaf nodes have teleportation portals, and the destination can be any leaf city in a country with an adjacent index. Each teleport takes $1$ unit of time, and each teleportation portal can be used only once. As shown in the figure below, if the starting point is $(0,2)$ and the destination is $(2,1)$, then $(0,2)\rightarrow(1,1)\rightarrow(1,0)\rightarrow(1,2)\rightarrow(2,1)$ is a feasible path, while $(0,2)\rightarrow(1,1)\rightarrow(2,1)$ is invalid, because the portal of $(1,1)$ was used once in $(0,2)\rightarrow(1,1)$ and again in $(1,1)\rightarrow(2,1)$.  Given the starting point and the destination, find the minimum time required.

The first line contains a positive integer $n$. Then there are $n$ blocks, each describing one country. The first line of each block is a positive integer $m_i$, indicating that the country with index $i$ contains $m_i$ cities. Then follow $m_{i}-1$ lines, each containing three integers $u, v, t$, meaning there is a road between city $u$ and city $v$, and the time cost is $t$ ($1 \leq t \leq 10^{3}$). The next line contains a positive integer $q$, the number of queries. Each of the next $q$ lines contains four integers $s_0, s_1, e_0, e_1$, where $(s_0, s_1)$ is the starting point and $(e_0, e_1)$ is the destination.

Output $q$ lines, each containing a single integer. If the destination is reachable from the starting point, output the minimum time; otherwise, output $-1$.

For $40\%$ of the testdata, $n \leq 10, \sum m_i \leq 10^{3}, q \leq 10$. For $60\%$ of the testdata, $n \leq 10^{3}, \sum m_i \leq 10^{6}$. For $100\%$ of the testdata, $n \leq 3.5 \times 10^{5}, \sum m_i \leq 10^{6}, 1 \leq t \leq 10^{3}, q \leq 10^{5}$. Translated by ChatGPT 5