P3900 [Hunan Training Camp] Tusen

There is a collection $S$ of strings; the concept of a collection here differs from the mathematical set in that duplicate elements are allowed (i.e., it is a multiset). Initially, $S$ contains $n$ strings $s_1, s_2, \cdots, s_n$. There are two operations: - Add to $S$ a string that already exists in $S$. - Select two strings from $S$, concatenate them, and add the resulting string to $S$. After performing any number of operations, among all strings in $S$, what is the maximum possible length of a palindromic substring? If the length can be infinite, output $\text{Infinity}$.

The first line contains an integer $n$, the initial size of the collection. Each of the next $n$ lines contains a string. The string on the $i$-th line is $s_i$. Each string contains only lowercase English letters.

If the maximum length of a palindromic substring is not infinite, output an integer representing its length; otherwise output $\text{Infinity}$.

#### Sample explanation In the first sample, concatenate $\text{ecab}$ and $\text{abacde}$ to get $\text{e}\underline{\text{cababac}}\text{de}$, where the underlined part is the longest palindromic substring of length $7$. It can be proven that no longer palindromic substring exists. In the second sample, you can concatenate arbitrarily many copies of $\text{ha}$ to obtain $\underline{\text{h}}\text{a},$ $\underline{\text{hah}}\text{a},$ $\underline{\text{hahah}}\text{a}$ and so on, yielding palindromic substrings of any odd length. Therefore the answer is infinite, so output $\text{Infinity}$. 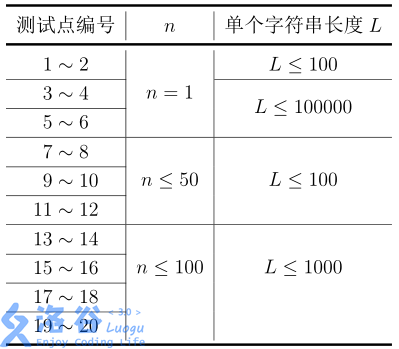#### Constraints  Translated by ChatGPT 5