P3906 Geodetic Set

A graph $\text G$ is an undirected connected graph with no self-loops, and there is at most one edge between any two vertices. We define the shortest path between vertices $v$ and $u$ as a path from $v$ to $u$ that uses the fewest edges. Every vertex that lies on some shortest $v$-$u$ path is called a $v$-$u$ Geodetic vertex, and the set of these vertices is denoted by $I(v,u)$. We call the set $I(v,u)$ a Geodetic set. For example, in the figure below, $I(2,5)=\{2,3,4,5\}$, $I(1,5)=\{1,3,5\}$, and $I(2,4)=\{2,4\}$.  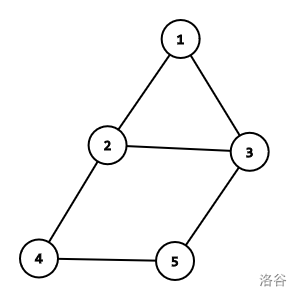Given a graph $\text G$ and several pairs $v, u$, please compute $I(v,u)$ for each pair.

The first line contains two integers $n, m$, representing the number of vertices and edges of $\text G$ (vertices are numbered $1 \sim n$). The next $m$ lines each contain two integers $a, b$, indicating that there is an undirected edge between vertices $a$ and $b$. The $(m+2)$-th line contains an integer $k$, representing the number of given pairs. The next $k$ lines each contain two integers $v, u$, the start and end vertices of each pair.

Output $k$ lines. For each pair $v, u$ in the input, output in one line all vertex indices in $I(v,u)$ in increasing order of vertex indices.

For all testdata, $1 \le n \le 40$, $1 \le m, k \le \frac{n(n-1)}{2}$. Translated by ChatGPT 5