P3925 aaa Gets "Xu"-ed

HansBug keeps being bored...

Because aaa did not finish HansBug's task, HansBug starts planning how to "xu" aaa. Now HansBug has $N$ aaa, each with a power value. There are $N - 1$ edges connecting pairs of aaa, so these $N$ aaa form a **rooted tree**, rooted at aaa $1$. HansBug wants to "xu" these $N$ aaa. His strategy is: for the $i$-th aaa, first let him and all of his descendant aaa ~~stand obediently ♂~~ in a queue, then "xu" them one by one. After long research on aaa power values, HansBug found that, for each such queue of aaa, suppose there are $n$ of them with power values $v_i$; then the power value gained from "xu"-ing the $i$-th aaa in the queue is $v_1 + v_2 + \cdots + v_i$. However, the relationship tree among aaa is quite complex, and HansBug has run out of IQ, so this task is handed over to you. But HansBug does know that no aaa has more than $5$ direct child aaa. HansBug wants to know, with the optimal queuing method each time, the maximum total power value obtainable after "xu"-ing all these aaa, ~~and then give you $100000 \% 10$ points of power value as a reward~~.

The first line contains a positive integer $N$, the number of aaa. The next $N - 1$ lines each contain two positive integers $u, v$, indicating that there is a subordinate relationship between the $u$-th aaa and the $v$-th aaa (the highest-level aaa is numbered $1$). The last line contains $N$ non-negative integers, where the $i$-th number is the power value of the $i$-th aaa.

Output a single integer, the maximum total power value HansBug can obtain after "xu"-ing all aaa. Since the result can be large, take it modulo $\bm{1000000007}$ ($\bm{{10} ^ 9 + 7}$).

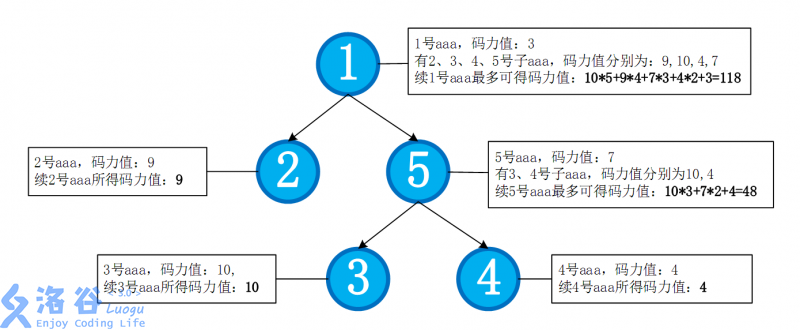
### Sample Explanation  Therefore, the maximum total power value from "xu"-ing $5$ aaa is $118 + 9 + 10 + 4 + 48 = 189$. After taking modulo $\bm{1000000007}$, the answer is $\bm{189}$. ### Constraints For $30\%$ of the testdata: $1 \leq N \leq 3 \times {10}^3$. For $50\%$ of the testdata: $1 \leq N \leq 2 \times {10}^4$. For $70\%$ of the testdata: $1 \leq N \leq {10}^5$. For $100\%$ of the testdata: $1 \leq N \leq 5 \times {10}^5$. For each aaa's power value $a_i$, it is guaranteed that $0 \leq a_i \leq {10}^8$. Translated by ChatGPT 5