P3940 Grouping

Large samples can be downloaded from the "Attachments" at the bottom of the page.

After learning the information she needed, Little C adjusted the rabbits to appropriate positions. She plans to divide the rabbits into several groups to feed them suitable carrots. At this moment, $n$ rabbits stand in a line in a fixed order. The $i$-th rabbit has color $a_i$. Since the order has been fixed, each group must be a contiguous segment in the sequence. Before grouping, Little C notices a pattern: some rabbits have pairwise conflicts. Two rabbits are in conflict if and only if the sum of their color values is a perfect square. For example, color 1 and color 2 do not conflict because 3 is not a perfect square; but color 1 and color 3 do conflict because $4 = 2^2$. Little C thinks it is fine as long as the conflict within a group is not too large. She defines the conflict value $k$ of a group as the minimum number of sub-teams into which this group must be further partitioned so that within each sub-team, any two rabbits do not conflict. These sub-teams do not need to be contiguous segments. Little C requires that the maximum conflict value among all groups does not exceed $K$. There may be many grouping methods that satisfy this. To make the grouping more harmonious, she wants to know, among all solutions with the minimum number of groups, which one is lexicographically smallest. Can you help her? The lexicographically smallest solution is defined as follows: list in increasing order all positions $i$ such that rabbit $i$ and rabbit $i + 1$ belong to different groups. Among all feasible solutions with the same number of groups, the one whose first differing position is smaller is considered lexicographically smaller.

Read from standard input. The first line contains two positive integers $n, K$. The second line contains $n$ positive integers; the $i$-th number denotes the color $a_i$ of the $i$-th rabbit.

Write to standard output. Print a single integer $m$ on the first line, the minimum number of groups you need to divide the rabbits into. Print $m - 1$ positive integers in increasing order on the second line. The $i$-th number $s_i$ means that $s_i$ and $s_i + 1$ are placed into different groups in your solution. If $m = 1$, then print an empty line.

[Sample 1 Explanation] If all five rabbits are put into one group, then the pairs (1, 3), (3, 6), (6, 10), (10, 15), (1, 15) cannot be placed in the same sub-team pairwise. Since at most two sub-teams are allowed, to satisfy the first four constraints, the only way is {{1, 6, 15}, {3, 10}}, but then (1, 15) is not satisfied. Therefore, there is no solution with $m = 1$ that satisfies all constraints. If the five rabbits are divided into two groups, one lexicographically smallest feasible grouping is {1}, {3, 15, 10, 6}. In this case, one way to partition the second group into at most 2 sub-teams is {{3, 10}, {15, 6}}. Constraints Subtasks will specify characteristics of some testdata. If you find the problem difficult, you may try to solve only part of the testdata. 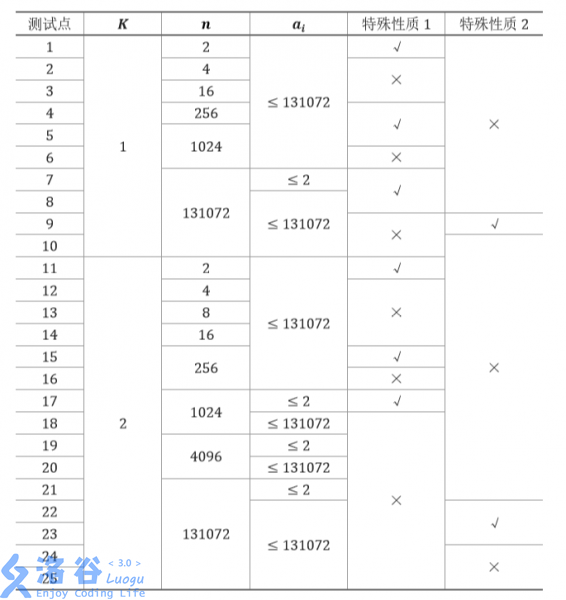The size and characteristics of each test point are shown in the table below:  Special property 1: The optimal grouping is guaranteed to be unique. Special property 2: No two rabbits share the same color. Translated by ChatGPT 5